목차
1. 분산분석이란?
분산분석은 다수( 2,3,4개 ..) 집단 간 평균을 비교한다.
독립변수 : 범주형
종속변수 : 연속형
2. 종류
영향을 주는 독립변수의 개수에 따라
| 1 | ANOVA | 일원배치 분산분석 |
| 2 | Two-way ANOVA | 이원배치 분산분석 |
| 3개 이상 | MANOVA | 다원배치 분산분석 |
※ 종속변수의 개수에 따라 아래와 같이 분류도 가능함.
1: 단일변량 분산분석
2개 이상: 다변량 분산분석
3. ANOVA 일원배치 분산분석
<실습>
1) EDA
import numpy as np
import pandas as pd
df=pd.read_csv('iris.csv')
df.head()
EDA를 해보자.
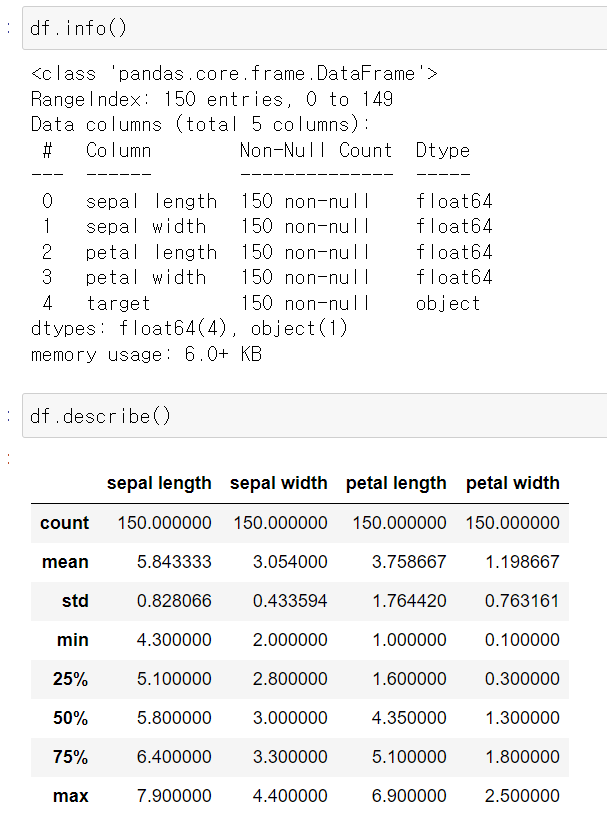
타겟 벨류가 세 가지가 있으며, 데이터는 균형적이다.

2) ANOVA
- 개념
<개념>
- 여러 개의 집단에서, 하나의 범주형 변수의 영향이 있는지 알아보는 검증 방법이다.
- 모집단의 수에는 제한이 없다.
- 각 집단의 표본 수는 같지 않아도 된다.
- F 검정 통계량을 이용한다.
독립 변수 세가지를 다시 한번 확인한다. 그리고 따로 집단을 만들어 준다.
- 범주형 독립변수: centosa, versicolor, virginica
- 연속형 종속변수: sepal width

시각화
seaborn을 이용해서 시각화한다.
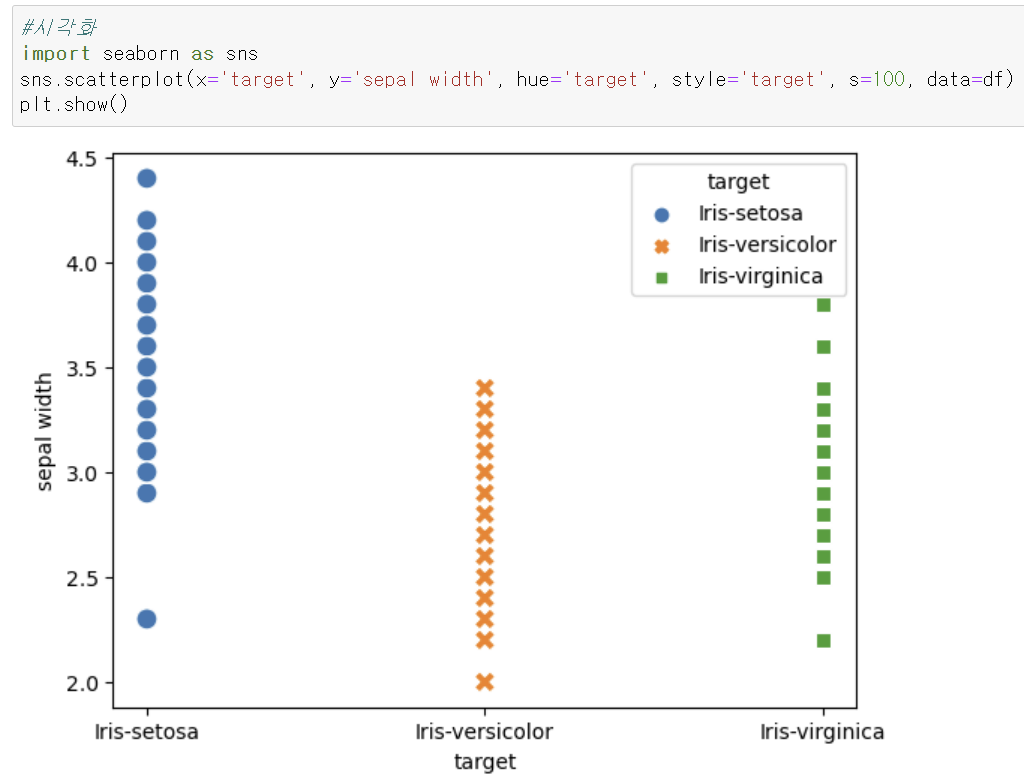
세 집단을 시각화해보았을 때, 각 집단의 분포가 차이가 있어보인다. 정확한 것은 F값으로 분산분석해서 통계적으로 검정하도록 한다.
가설설정
H0: 세 집단의 Sepal width에 관한 평균은 모두 같다
H1: 적어도 하나의 종에 대한 Sepal width 평균은 차이가 있다.
그 전에 아래의 두 가지 가정이 만족하는지 확인한다.
<가정>
- 집단의 측정치는 서로 독립이며 정규분포를 따른다.
- 집단 측정치의 분산은 같다.(등분산)
1) 정규성 검정
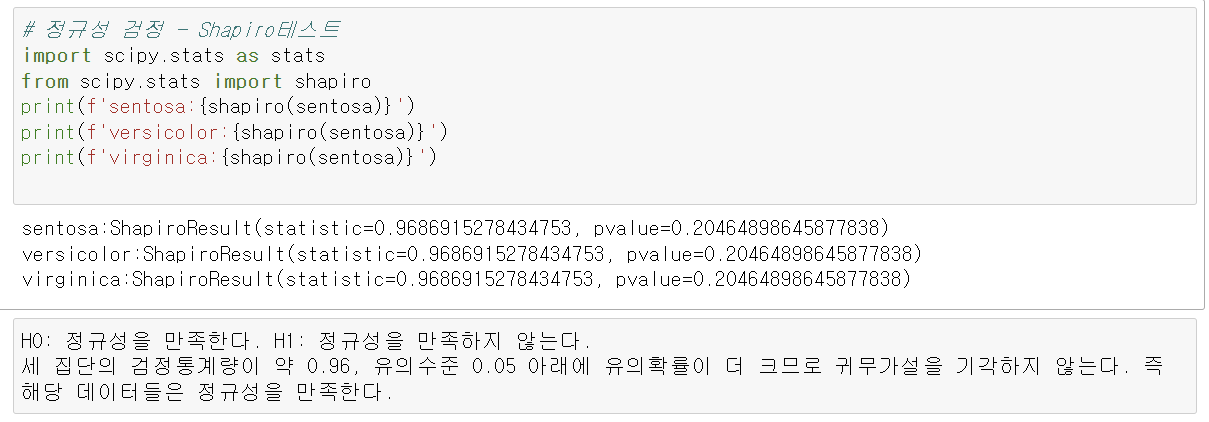
2) 등분산성 검정

ANOVA test
stats.f_oneway(sentosa, versicolor, virginica)세 집단 데이터의 f값은 (집단간평균/집단내평균)이다. 검정통계량은 47.36이고 유의수준 0.05 아래 pvalue는 유의수준보다 크므로, 세 가지 종의 sepal width의 평균은 유의미한 차이가 있다고 볼 수 있다.
※ F-value란?
- 평균의 차이의 계산이 아니라, 분산의 비율값이다.
- 집단 간 평균 제곱/ 집단 내 평균 제곱
- 집단 간 분산이 크면 f가 커진다.
- 집단 내 분산이 작으면 f가 커진다.
- f가 크면, 해당 집단 간의 차이가 있다고 할 근거가 확실해지므로 귀무가설을 기각할 확률이 높아진다.
사후검정
여기서 끝이 아니다. 사후검정을 진행한다.
※ 사후검정(Post Hoc Test)
- 분산분석의 결과 귀무가설이 기각되어 적어도 한 집단에서 평균의 차이가 있다는 것이 통계적으로 증명된 후 하는 검정이다.
- 어떤 집단들에 대해서 평균의 차이가 존재하는지 알아본다.
- 종류: 던칸의 MRT, vltudml LSD, 튜키의 HSD방법
튜키의 HSD
* 튜키의 HSD(Honest Significant Difference) test 방법
여러 그룹 간의 평균 차이를 비교하여 각 그룹 차이가 통계적으로 유의미한지 확인하는데 사용됨
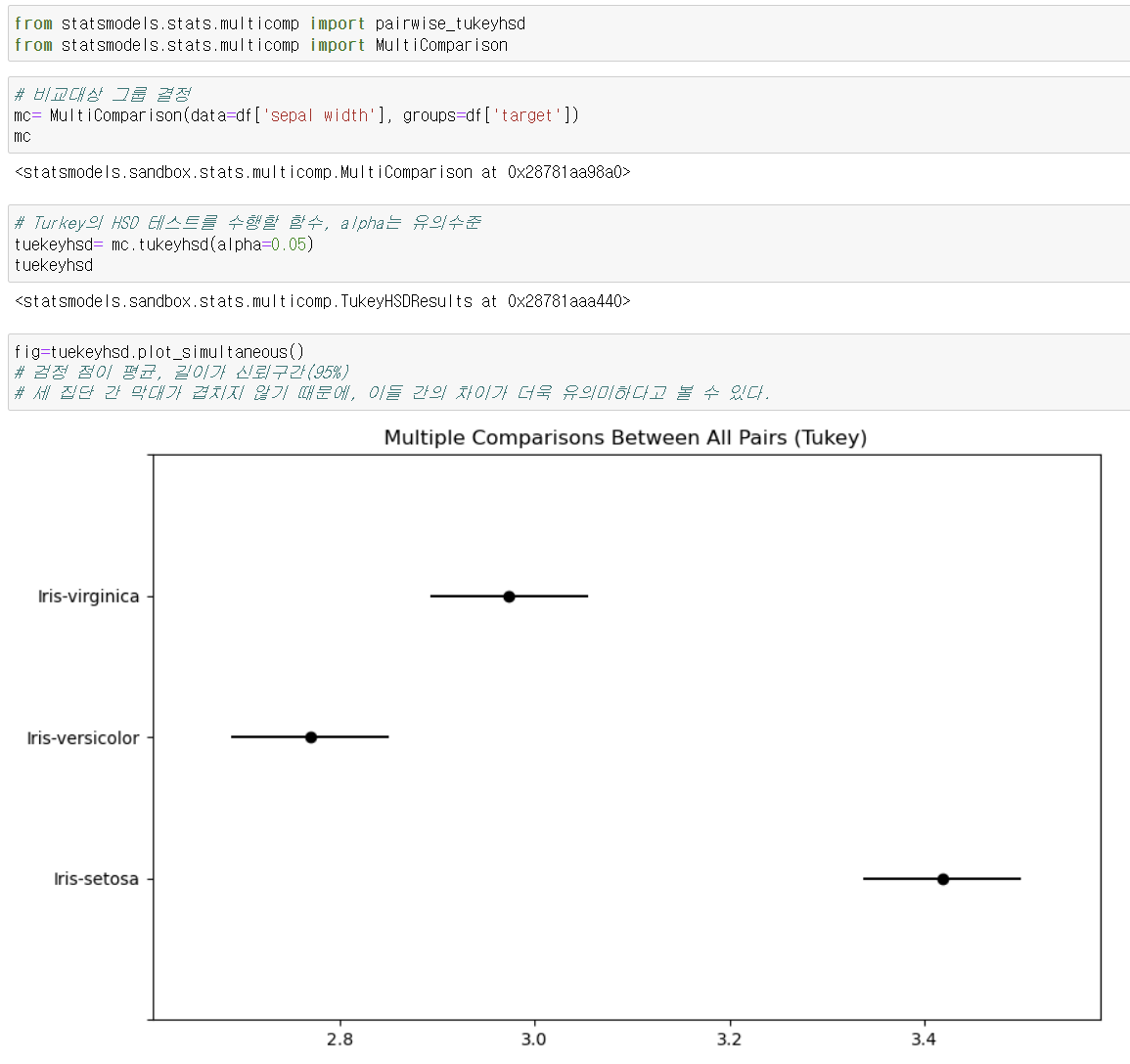
tuekeyhsd를 summary()해보자.
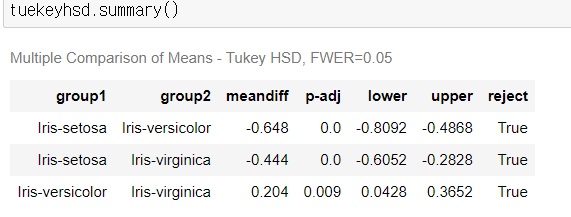
# Mean difference: 그룹 간의 평균 차이 group2- group1
# p-adj = p value
# lower-upper 신뢰구간의 하한-상한
# reject True: 해당 그룹 간의 평균 차이가 통계적으로 유의미하다.
Kruskal, welch ANOVA
이제까지는 정규성과 등분산성을 만족한다는 가정 아래 수행했다.
하지만 정규성과 등분산성을 만족하지 않는다면 어떨까?
1) 정규성 만족하지 않는다면?
--> Kruskal ANOVA
- 비모수적 통계 검정 방법 중 하나로, 세 개 이상의 독립적인 그룹 간의 평균 순위 차이를 비교하는 데 사용된다.
- 모든 그룹에서 정규 분포를 가정하지 않고, 그룹 간의 분산이 다를 수 있다는 가정 하에 작동한다.
stats.kruskal(sentosa, versicolor, virginica)
2) 등분산성 만족하지 않는다면?
--> welch ANOVA
- ANOVA의 한 형태로 세 개 집단이 등분산성이 만족되지 않을 때 그룹 간의 차이를 검정하는 방법이다.
- 비모수 검정이 아니다.
- 혼재분산 문제를 해결한다.
- F 통계량을 사용한다.
! pip install pingouin
# dv: 종속변수, betwwen: 독립변수, 그룹변수
import pingouin as pg
pg.welch_anova(data= df, dv='sepal width', between='target')
- source: 분석된 데이터에서 발생한 변동 요소
- ddof1: source의 자유도= sorce그룹수-1
- ddof2: error의 자유도=총샘플 수-총 그룹 수
- f : 그룹간의분산/그룹내분산= f값이 클 수록 그룹 간의 차이가 크다는 의미
- p-unc: p_value f통계량에 대한 p값. 귀무가설을 설정했을 때 해당 통계량을 얻을 확률. p값은 귀무가설을 기각하고 대립가설을 지지하는 증거가 된다.
- np2: 효과 크기 지표, 그룹간의 변동/전체 변동, 값이 클 수록 그룹 간의 차이가 크다.
4. 이원배치 분산분석 Two-way ANOVA
1) 개념
- 독립변수: 범주형(수치형이라도 상관없음, 범주형의 형태면 됨)
- 종속변수: 연속형
- 분산분석에서 하나의 종속변수(연속형)에 대한 두 개의 독립변수(범주형) A,B의 영향을 알아보기 위한 검증 방법
ex) 재산, 지역에 따른 수능점수의 차이 검정
- 두 독립변수 A, B 사이에 교호작용 검증이 반드시 있어야 함
§ 교호작용
두 개 이상의 변수가 함께 작용할 때 나타나는 현상, 두 변수들이 서로 영향을 주고받는 상호작용을 나타냄.
ex) 농구경기분석 A: 선수의 실력 B:바구니까지의 거리
- A,B 사이의 교호작용을 생각해보자면, 두 변수가 함께 작용할 때 어떤 일이 일어나는지 설명하는 것이다.
- 선수의 실력이 높고, 바구니까지 거리가 가까우면 선수는 더 쉽게 골을 넣을 것이다. --> 양의 교호작용
- 선수의 실력이 낮고 바구니까지 거리가 멀면 선수는 골을 넣기가 어려울 것이다. --> 음의 교호작용
---> 교호작용이 없는 경우에는 각 독립 변수의 주효과만을 고려하여 종속 변수와의 관계를 분석한다.
2) 가정
a. 정규성 : 각 집단 측정치의 분포는 정규분포를 따른다.
b. 등분산성 : 집단 간 측정치의 분산은 같다.
3) 가설설정
Two-way ANOVA는 교호작용 검정과 주효과 검정을 수행한다.
그래서 총 6가지 가설이 있다.
3개의 귀무가설과 3개의 대립가설이다.
<실습>
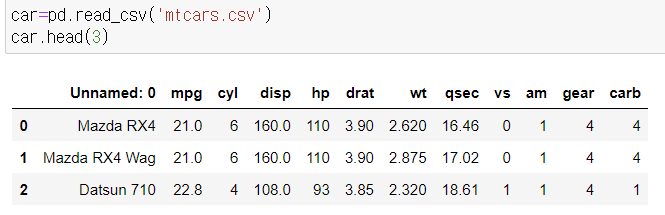
데이터 EDA
mpg - Miles per Gallon 마일 효율성
cyl - # of cylinders 엔진 실린더수
disp - displacement, in cubic inches
hp - horsepower
drat - driveshaft ratio (don't really KNOW cars, so if you've got questions - you know what to do. :-D
wt - weight
qsec - 1/4 mile time; a measure of acceleration
vs - 'V' or straight - engine shape
am - transmission; auto or manual변속기 형태
gear - # of gears
carb - # of carburetors.
여기서 변속기와 실린더를 독립변수로, 마일효율성을 종속변수로 둔다.
#am 변속기 cyl 실린더 mpg 마일효율성
mtcar= car[["mpg", "cyl", "am"]]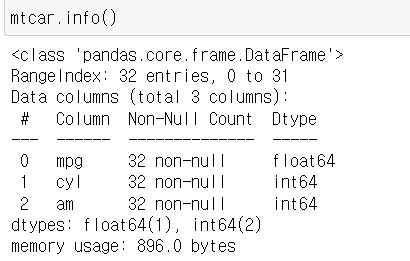

교호작용 검정
<교호작용 검정>
여러 독립변수들의 조합이 종속변수에 주는 영향이다. 즉, 한 독립변수가 종속변수에 미치는 영향이 다른 독립변수의 수준에 따라서 달라지는 지를 분석하는 것이다.
- 두 독립변수 사이에 상관관계가 존재하면 교호작용이 있다.
- 교호작용이 없으면 주효과 검정을 진행한다.
- 교호작용이 있으면 검정이 무의미하다.
H0: a와 b 변수의 교호작용이 없다.
H1: a와 b 변수의 교호작용이 있다.
ex) 성별과 학년에 따른 점수에 대한 데이터이다.
| 성별 /학년 | 1 | 2 | 3 |
| 남 | 60 | 70 | 80 |
| 여 | 50 | 40 | 60 |
그래프를 그려보면 두 데이터 사이에 교차되는 지점이 없다. 따라서 교호작용이 없다고 본다.
주효과 검정
<주효과 검정>
주효과란 각각의 독립변수가 종속변수에 미치는 영향을 의미한다. 이를 검정하는 것을 주효과 검정이라 한다.
<주효과 검정1>
H0: a변수에 따른 종속변수 값에는 차이가 없다.
H1: a변수에 따른 종속변수 값에는 차이가 있다.
<주효과 검정2>
H0: b변수에 따른 종속변수 값에는 차이가 없다.
H1: b변수에 따른 종속변수 값에는 차이가 있다.
<실습>
두 독립변수 간, 교호작용이 있는지 확인하고 주효과 검정을 해보자.
Two-way ANOVA 모델을 생성하기 위해, formula를 만든다.
formula는 model = ols('mpg~ C(cyl)*C(am)', mtcar).fit() 처럼 만들어도 된다.
ANOVA를 실행한다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# Two-way ANOVA 모델 생성
# C() 함수는 범주형 변수
formula= 'mpg ~ C(cyl) + C(am) + C(cyl):C(am)'
model = ols(formula, mtcar).fit()
# ANOVA 수행, typ=2: 2원배치
aov_table= anova_lm(model, typ=2)
aov_table
결과를 해석해보자.
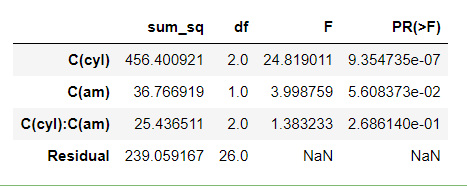
1) cyl과 am 간에는 교호작용이 없다. p value가 0.26이므로 0.05보다 크므로 귀무가설 기각하지 않음.
--> 두 변수 사이에 교호작용이 없기 때문에 아래와 같은 주효과 검정이 의미를 갖는다.
2) cyl 변수에 대한 pvalue는 0.05보다 작다. 귀무가설을 기각한다.
--> cyl은 mpg 사이에 유의한 차이가 있다.
3) am 변수에 대한 pvalue는 0.056이므로 0.05보다 크다. 귀무가설을 기각하지 못한다.
--> am에 따른 mpg 차이는 존재하지 않는다.
시각화
시각화해서 교호작용이 있는지 없는지 확인해보자.
interaction plot을 그릴 때 주의할 점은, 매개변수를 x1, x2, y 순으로 작성한다는 점이다.
#시각화 : 교호작용 그래프 그리기
from statsmodels.graphics.factorplots import interaction_plot
import matplotlib.pyplot as plt
# interaction_plot의 매개변수는 x1, x2, y 순으로 작성한다.
cyl=mtcar["cyl"]
am=mtcar["am"]
mpg=mtcar["mpg"]
fig, ax= plt.subplots(figsize=(6,6))
fig = interaction_plot(cyl, am, mpg,
colors=['red', 'blue'], markers=['D', '^'],
ms=10, ax=ax)
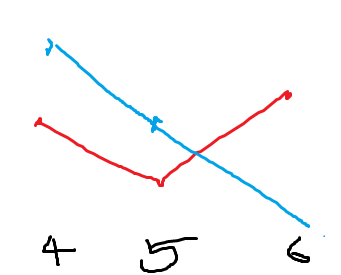
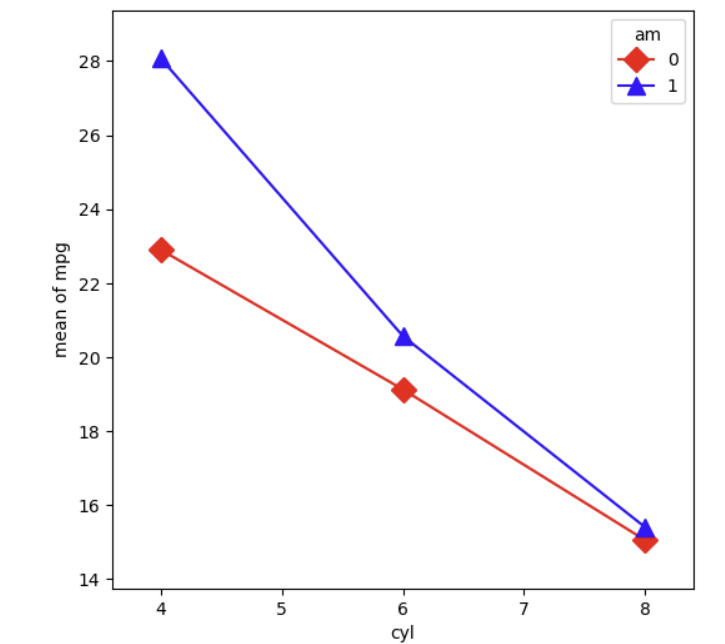
결과를 해석해보자면, 상호작용 그래프에서 두 선이 서로 교차하고 있지 않기 때문에 시각화된 독립변수 cyl, am 사이에는 상호작용이 존재하지 않는다고 본다.
만약 그래프가 아래와 같다면 교호작용이 있다. 이럴 때는 cyl가 4, 5일 때는 교호작용이 없으므로 am에 따른 mpg의 평균의 차이가 없지만, cyl 6일 때는 am에 따른 mpg의 평균의 차이가 존재한다. 다시 말해, cyl 6일 때는 am=1일 때보다 0일 때 mpg의 평균이 크다.