목차
DBSCAN
- Density based Spatial Clustering of Application with Noise
- 밀도 기반 군집화의 대표 알고리즘으로 데이터 분포가 기하학적으로 복잡한 데이터 세트에 효과적임

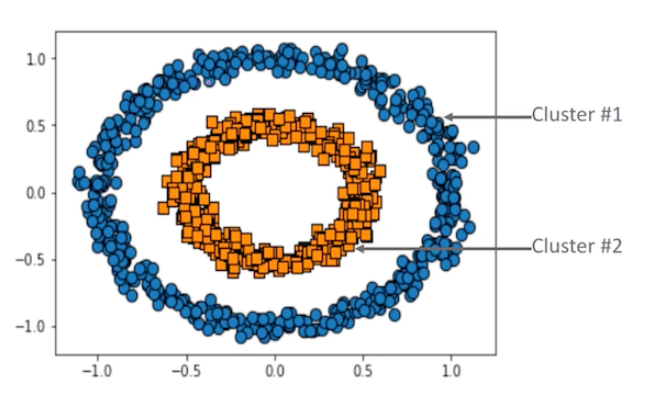
- 높은 밀도의 데이터 포인트의 군집을 형성하고, 밀도 낮은 지역은 노이즈 처리
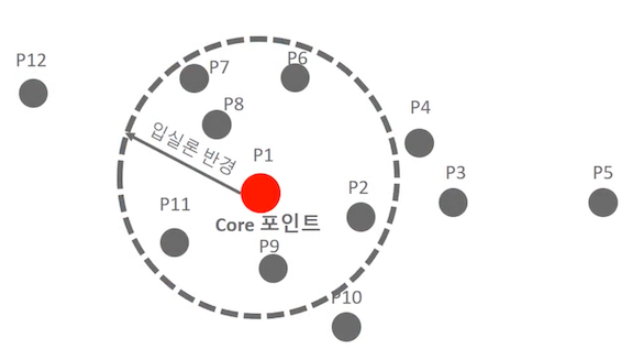
- 입실론 주변 영역의 최소 데이터 개수를 포함하는 밀도 기준을 충족시키는 데이터인 핵심 포인트를 연결하면서 군집화를 구성하는 방식
- 알고리즘이 클러스터 개수 자동 지정
- 입실론 eps : 주변 영역의 반경(얼마나 가까운 얘들을 같은 클러스터로 묶을 것인가)
- Min Pts : 해당 영역 내에 존재하는 최소 데이터 포인트 수 (적어도 몇 개 이상을 하나의 클러스터로 묶겠다는 뜻)
- 나머지 : 노이즈 처리

| 핵심 포인트 | 이웃 포인트 | 경계 포인트 | 노이즈 |
| 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 가진 경우 | 주변 영역 내에 위치한 타데이터 | 주변 영역 내에 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지는 않지만, 핵심 포인트를 이웃 포인트로 가지고 있는 데이터 | 최소 데이터 개수 이상의 이웃 포인트도 없고, 핵심포인트도 이웃포인트가 아닌 데이터 |
<실습>
모델생성

시각화

GMM(Gaussian Mixture Model)
- 혼합분포군집
- 모형(model) 기반 군집방법
- GMM 군집화는 군집화를 적용하고자 하는 데이터가 여러 개의 가우시안분포(정규분포)를 가진 데이터 집합들이 섞여서 생성된 것이라는 가정하에 군집화 수행하는 방식
- 100개의 데이터세트가 있다면 이를 구성하는 여러 개의 정규 분포 곡선을 추출하고, 개별 데이터가 이 중 어떤 정규분포에 속하는지 결정하는 방식
- 모수 추정
- 1) 개별 정규 분포의 평균과 분산
- 2) 각 데이터가 어떤 정규분포에 해당하는지의 확률

- 사용하는 이유
- 실생활 데이터에 적용시키기 위함
- 대부분의 실생활 데이터는 정규분포 형태이기 때문
- EM알고리즘 사용(Expectation and Maximization) : 최대가능도(liklihood)가 최대인가?
- 설명할 수 있는 데이터의 형태: 다봉형(실생활데이터가 많이 취하는 모양)

- 장점
- 확률분포를 도입했기 때문에 kmeans보다 통계적으로 엄밀한 결과를 얻을 수 있음
- 군집을 몇 개의 모수로 표현할 수 있고, 서로 다른 크기나 모양의 군집을 찾을 수 있음
- kmeans보다 유연하게 다양한 데이터세트에 잘 적용됨
- Kmeans는 원형 형태의 데이터에서는 군집을 잘하지만, 길쭉한 타원형 등의 데이터에서는 잘 못하기 때문
- 단점
- 군집의 크기가 너무 작으면 추정의 정도가 떨어짐
- 데이터가 커지면 EM 알고리즘 적용시 시간/계송비용 증가
- 이상치 처리를 잘해야 함
- 유형들의 분포가 정규분포와 차이가 크면 결과가 좋지 못하다.
- 몇 개의 확률분포를 혼합할 것인지 사용자가 지정하면 그 개수에 맞춰서 모델이 만들어짐
<실습>
데이터 정규화

가우시안 혼합모델 구축
- n_components 모델의 총 개수(사용자 설정)

시각화
