목차
통계분석방법
자료의 속성과 분석 목적에 따라 달라진다.
자료
variation 변동을 표현하는 중요한 수단으로, 좁은 의미에서는 숫자들을 모아놓은 집합이다.
빅데티어 시대에는 다양한 형태(이미지, 텍스트, 영상)의 자료가 쏟아져 나오기 때문에 이를 분석하려는 요구가 증가하고 있다. 비정형 자료는 각종 전처리 작업으로 자료를 정형화시켜 숫자로 만들어 통계분석에 활용한다.


1) 양적 자료: 연속형(셀 수 없음), 이산형 자료(셀 수 있음)--> 수치로 표현할 수 있음
- 이산형자료(discrete data): 관측값들을 셀 수 있는 자료 (예) 교통사고 건수, 자녀수, 에어컨 생산대수 등
- 연속형자료(continuous data): 관측값들을 셀 수 없고 연속적인 구간의 값을 갖는 자료 (예) 신장이나 체중, 체질량지수, 소득, 예금 잔액 등
2) 질적 자료: 명목형(순서의미x), 순서형 자료-->어떤 속성(범주)를 나타낸 자료로 범주형 자료--->수치로 표현 X
-명목형자료(nomial data): 순서에 의미가 없는 자료 (예) 성별(남/여), 혈액형(A형/B형/O형/AB형), 생존여부 등
- 순서형자료(ordinal data): 순서에 의미가 있는 자료 (예) 순위(1등,2등,3등),학점(A학점/B학점/…/F학점),비만도(과체중/보통/저체중)
변수 variable
조사대상(관찰개체)의 특성
- 사람일 경우 변수는 키, 몸무게, IQ, 수입, 학력 등
- 기업일 경우 변수는 매출액, 종사자수, 자본금, 주가 등
- 꽃일 경우 변수는 꽃잎의 너비, 줄기의 길이, 뿌리의 길이
1)일변량 자료 univariate data
2)이변량 자료 bivariae data
3)다변량 자료 multivariate data
다변량 자료는 각 기본단위에 변수가 두 개 이상이므로 일변량 자료에서 얻는 특성 외에 변수간의 관계, 변수간의 밀접성, 한 변수의 값이 주어질 때 다른 변수의 값에 대한 예측 등을 밝히는 통계분석이 사용될 수 있다. 일반적으로 자료는 다변량 자료이며 각각의 관심 있는 변수에 따라 통계분석을 수행할 수 있다. 특정 관심 변수에 대한 분석을 할 때, 그 변수만을 사용하여 분석을 하면 일변량 분석이라 하며, 그 변수 이외의 다른 변수들의 관계를 고려하여 같이 분석을 하면 다변량 분석이라 한다. 예를 들면, 상위 100대 기업의 매출액 에 관심이 있을 때,
- 일변량 분석: 100대 기업의 매출액의 평균, 분산, 중위수, 분위수 등을 매출액 변수자체만을 가지고 분석 할 경우
- 다변량 분석: 매출액에 영향을 미치는 다른 변수(기업규모, 주가, 투자금 등)를 고려하여 분석할 경우

-중간고사, 기말고사 양적변수
- 학과, 성별: 질적변수-명목---> 시각화할 때 막대그래프, 원그래프로 표현
- 학년:질적변수-순서형
시각화

막대그래프
표현 값에 비례하여 높이와 길이를 지닌 직사각형 막대로 범주형 데이터를 표현하는 차트나 그래프를 말한다. 막대그래프 를 그릴 때에는 빈도 또는 백분율을 이용하며 일반적으로 빈도를 더 많이 사용한다.
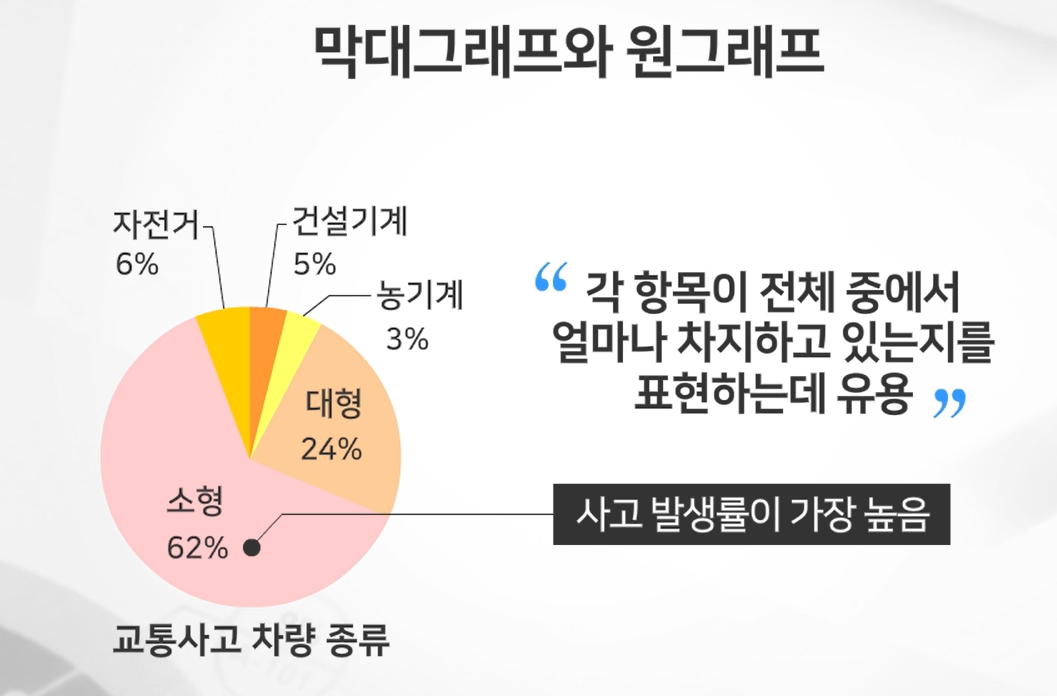
원그래프
각 항목이 전체 중에서 얼마나 차지하고 있는지를 표현하는 데에 유용하다.
도수분포표
한편, 연속형자료는 일반적으로 실수 전체를 가질 수 있다. 이러한 연속형 자료를 가지고는 단순 도수분포표를 이용한 막대그래프나 원그래프를 그리 는 것은 의미가 없다. 따라서, 연속형 자료에서는 관측값들을 몇 개의 구간으로 나누고 각 구간의 빈도를 나타 낸 도수분포표를 이용하여 자료를 요약할 수 있고, 히스토그램이라는 그림을 그려 자료의 특성 및 분포를 파악하는 것이 좋다.
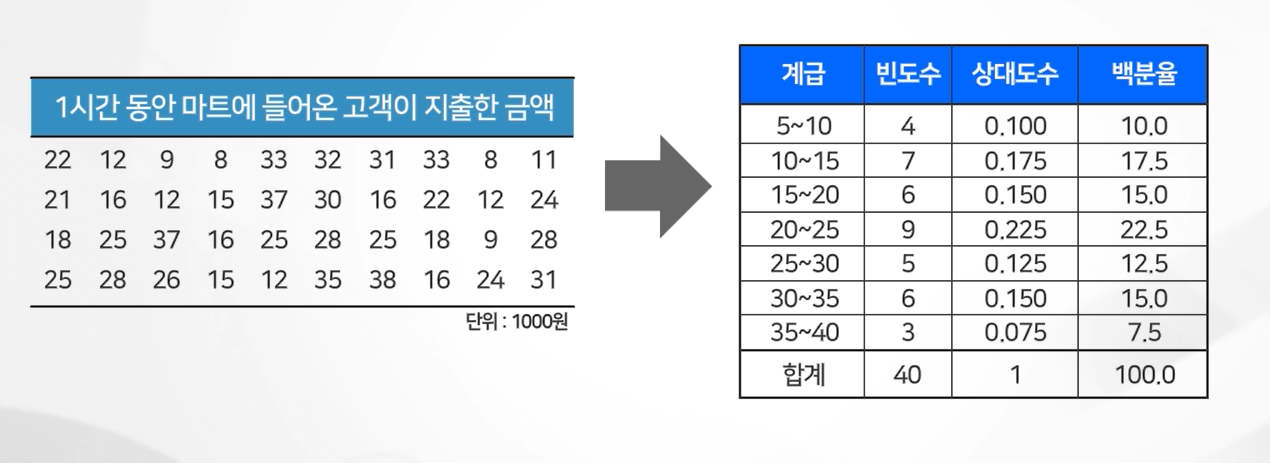
자료의 값과 도수를 정리한 표이다. 그런데 관측값이 많고 서로 다른 관측값들이 많은 자료에 대해서는 개개의 관측값에 대한 도수분포를 작성하기 어렵다. 이런 상황에서는 관측값을 몇 개의 구간으로 나누 고 나누어진 각 구간에 속하는 자료가 몇 개인지로 기록하는 것이 편리하다. 도수분포표를 이용하면 개별적인 데이터를 보는 것 보다 데이터의 전체적인 분포를 요약해서 볼 수 있다
히스토그램
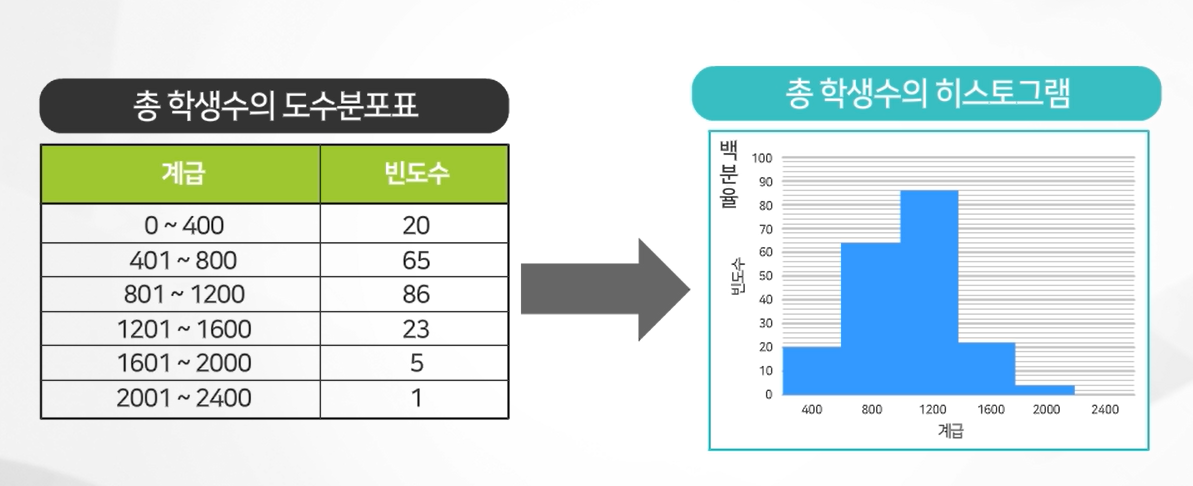
히스토그램은 구간의 빈도나 백분율을 이용하여 작성하며 x축은 자료의 구간, y축은 각 구간의 빈도(혹은 백분 율)가 된다. 막대그래프와는 다르게 구간의 값이 연속적이기 때문에 막대들 간의 간격이 없어야 한다.
줄기-잎 그림 stem and leaf plot
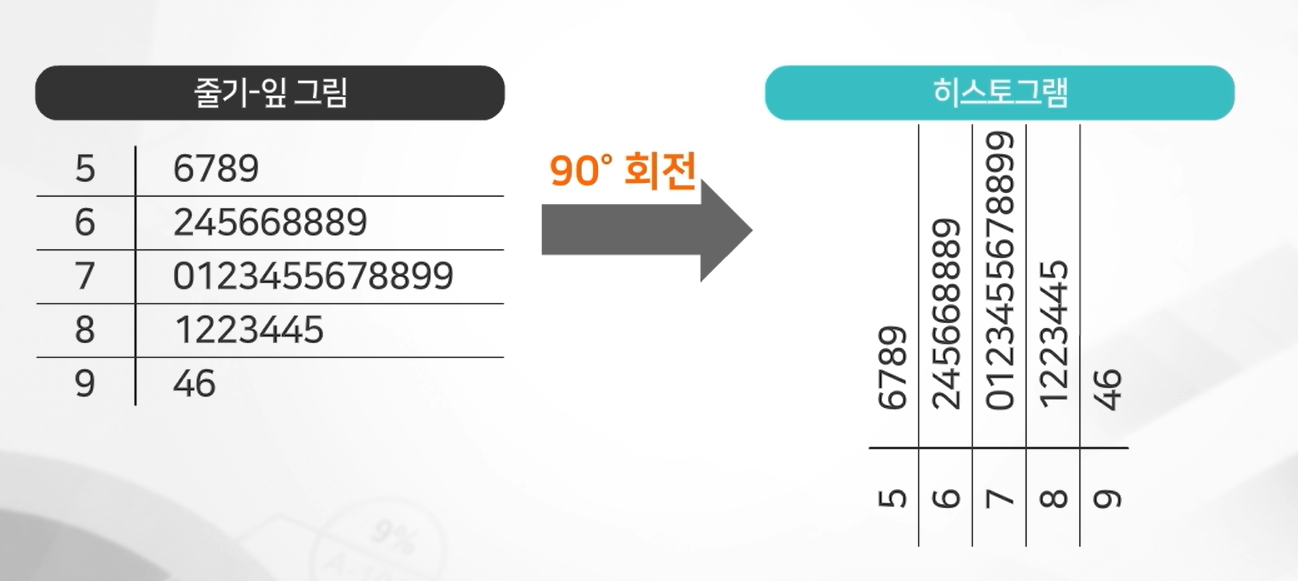
각 관측값을 줄기(stem)와 잎(leaf) 두 부분으로 나눈다. 관측값이 두 자릿수이므로 십단위를 줄기, 일단위를 잎으로 한다. 일반적으로 줄기는 두 자릿수 이상이 될 수 있지만 잎은 한 자릿수이어야 한다. 예를 들어, 82은 줄기가 8이고 잎이 2이다. 줄기 값을 세로로 작은 것부터 쓰고, 줄기 옆에 직선을 긋는다.
사분위수
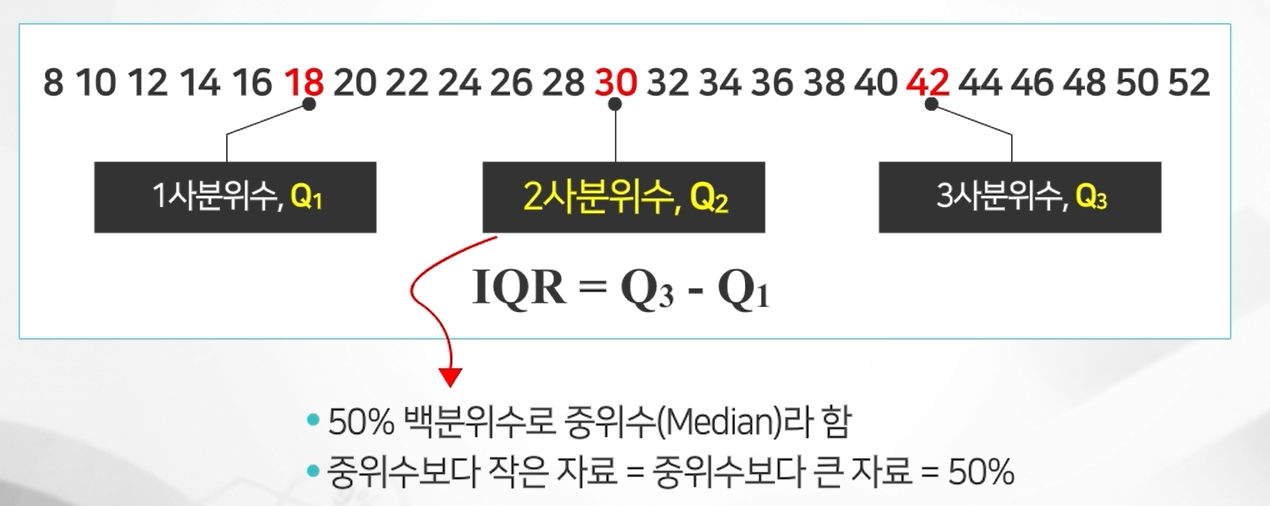
상자그림
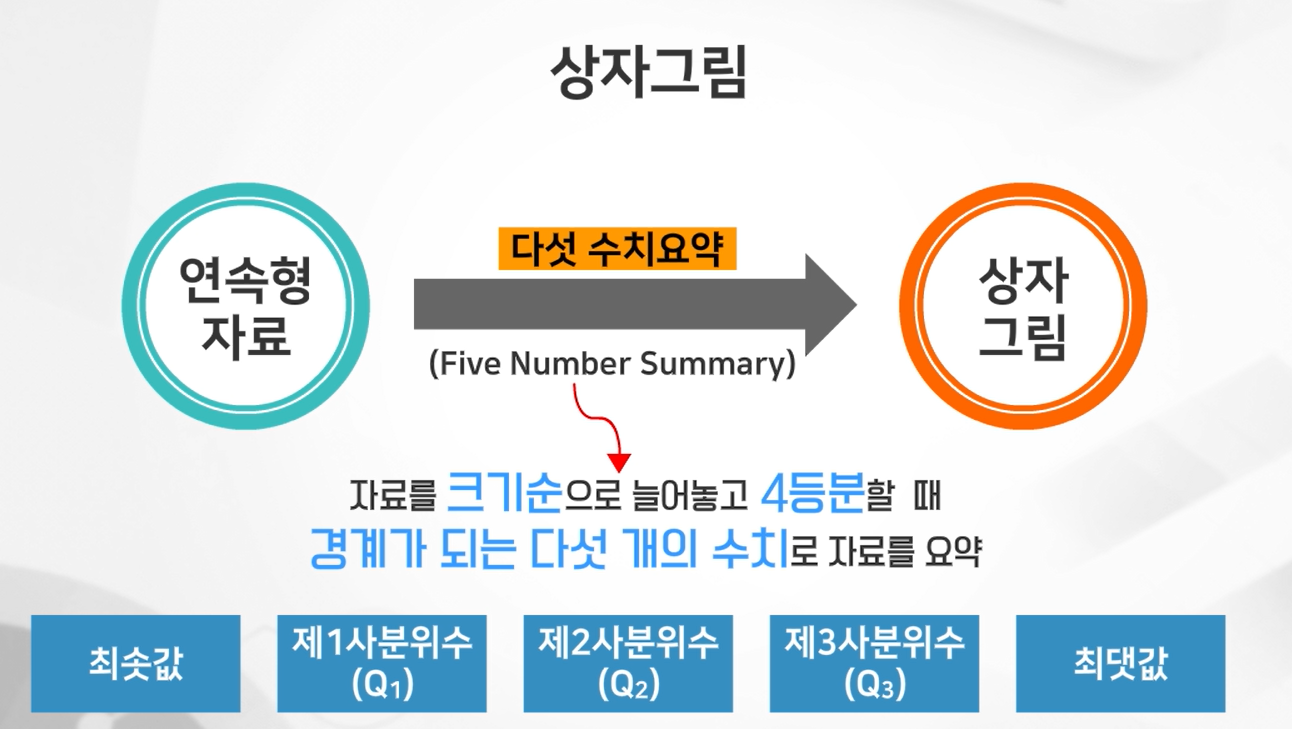
five number summary 다섯 수치요약
: Q1, Q2, Q3, 최솟값, 최댓값
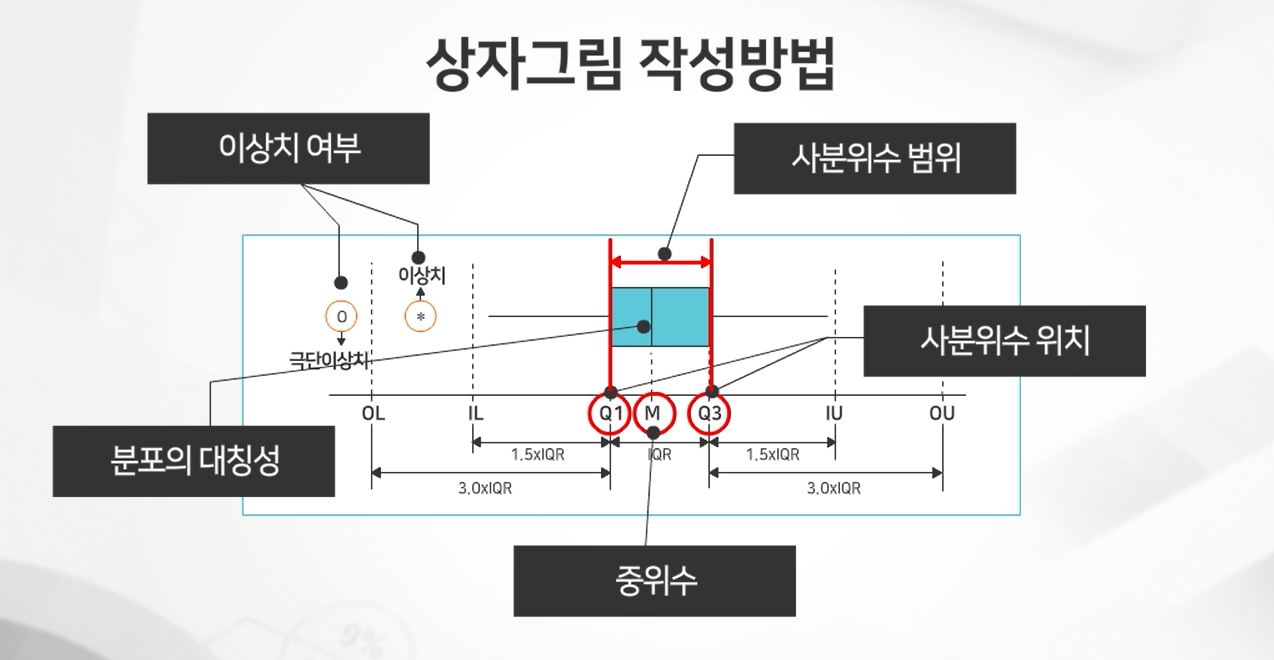
- 다섯 수치요약을 구한다.
- 두 사분위수에 해당하는 수직선상의 위치에 네모 형 상자의 양 끝이 오도록 상자를 그리고, 상자 안에서 중위 수에 해당하는 위치에 선을 긋는다.
- 두 사분위수의 차이 IQR=Q3-Q1(이것을 사분위 범위라 함)을 계산하고
- 두 개의 안쪽 울타리(inner fence) 값 IL, IU와
- 두 개의 바깥울타리(outer fence) 값 OL, OU를 계산한다.

- 양쪽 안쪽 울타리의 안에 있거나 안쪽 울타리 값과 같은 관측 값 중 안쪽 울타리 값에 가장 가까운 관측 값을 각각 찾아낸다. 이 관측 값을 인접 값이라 하고 AL과 AU로 표시한다. 상자 양 끝에서 두 인접 값 AL, AU의 위치까지 선으로 연결한다.
- 안쪽 울타리와 바깥울타리 사이에 관측 값이 있으면 그들을 이상치로 분류하고 그 위치에 ‘*’표시를 한다.
- 바깥울타리의 밖에 관측 값이 있으면 그들을 극단 이상치로 분류하고 그 위치에 ‘o’표시를 한다.
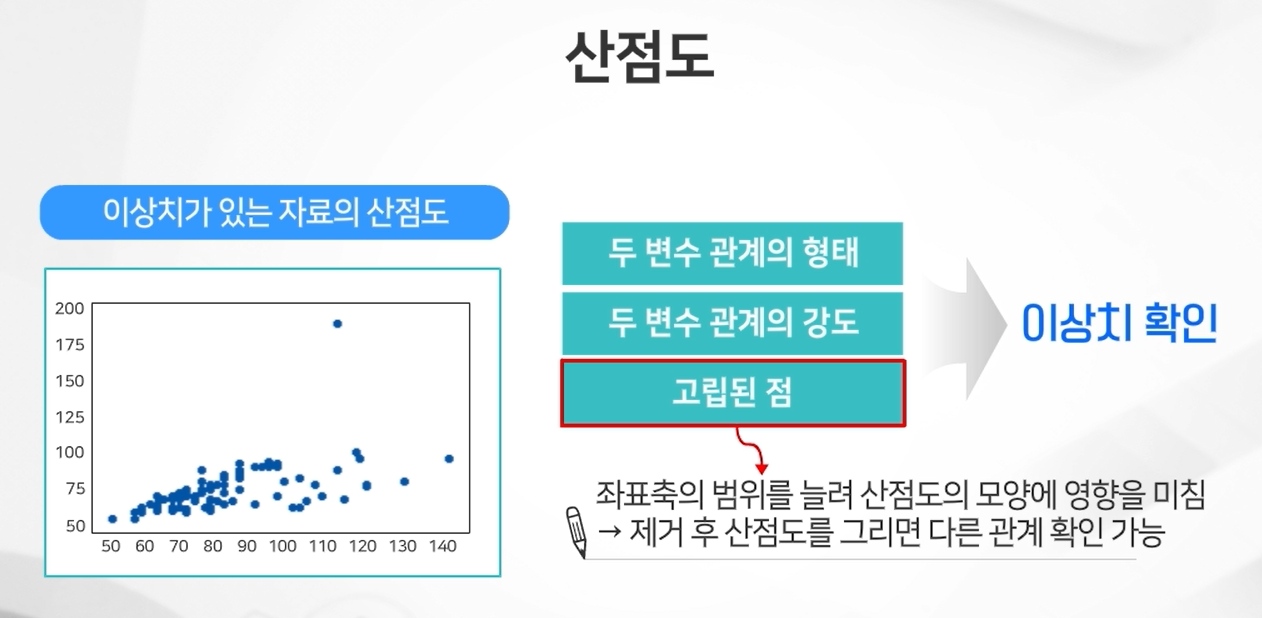
산점도 scatter plot
이변량자료에서 두 변수 간의 관계를 효과적으로 보여준다.
각 변수간의 관계와 강도를 알 수 있고,
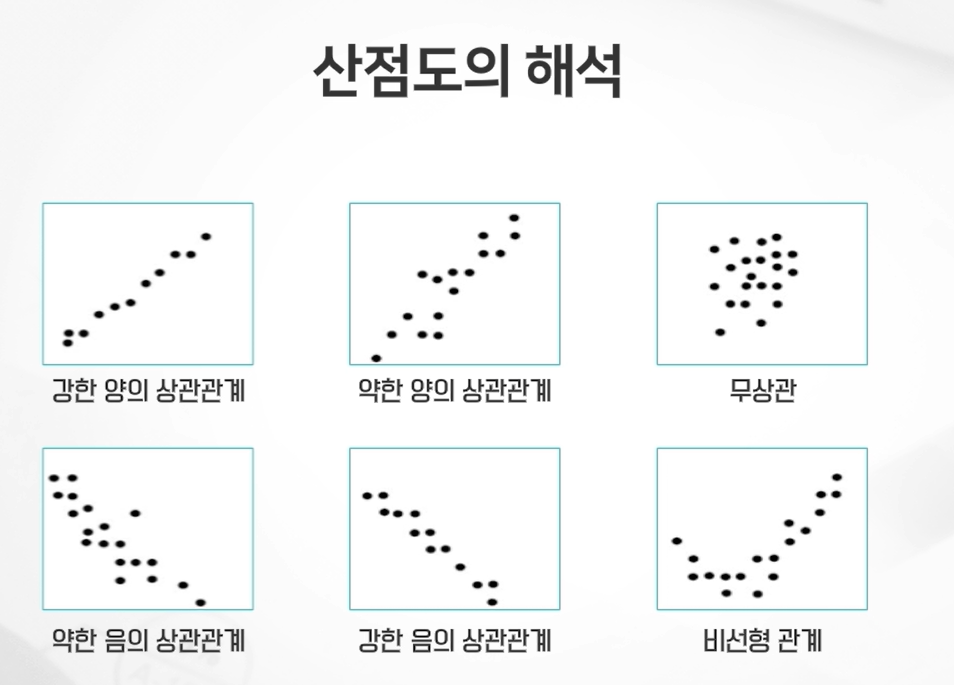
고립된 점으로 이상치를 확인할 수도 있다.
'Certificate > 통계학' 카테고리의 다른 글
| [통계] 확률론, 확률실험, 표본공간, 사상, 여사상, 배반사상, 독립사상, 순열, 조합, 조건부 확률, 전확률, 베이즈정리 (0) | 2023.05.09 |
|---|---|
| [통계] 산포도, 범위, 사분위수 범위, 분산, 표준편차, 모분산, 표본분산, 표본분산 n-1, 변동계수 (0) | 2023.05.09 |
| [통계] 대푯값, 산술평균, 중위수, 최빈값, 기하평균, 조화평균, 절사평균 (0) | 2023.05.09 |
| [통계] 표본조사, 표본추출, 표본오차, 비표본오차, 단순랜덤추출법, 층화랜덤추출법, 집락추출법, 계통추출법 (0) | 2023.05.09 |
| [통계] 통계학, 모집단, 표본, 모수 , 통계량, 통계치, 기술 통계학, 추측 통계학 (0) | 2023.05.09 |