목차

회귀분석
- 목적: 독립변수와 종속변수 간에 어떤 관계가 있는지 아는 것
< 용어 >
| 변수 | ||
| ★ Continuous variables | Takes on any real value between minum and maximum value. | 연속형 변수 |
| ★ Categorical Variables | Have a finite number of possible values | 범주형 변수 |
| ★ dependent variable.=Y | response or outcome variable | 종속변수 |
| ★ Independet variable=X | A variable that explains trends in the dependent variable = explanatory or predictor variable. |
독립변수 |
| 수학적인 이해 | ||
| ★ Slope | The amount that y increases or decreases per one-nuit increase of x | 기울기 |
| ★ intercept | x가 0일 때 y의 값 | 절편 |
| ★ Observed values vs actual values | 모집단(actual values)을 모두 알기란 현실성이 없다. 따라서 모집단을 대표하는 샘플(observed values)로 회귀모델을 만들 것이다. | |
| ★ Parameter vs Regression Coefficient (slope, intercept) |
모집단을 다 확인할 수 없으니 샘플들로 parameter을 추정한다. 하지만 이 값이 모집단의 파라미터와 같은지 100% 확실할 수 없다. 즉, 오차가 존재한다는 의미이다. | |


| ★ Loss function | A function that measures the distance between the observed values and the model's estimated value | 손실함수를 최소로 하는 가장 적합한 선을 찾는다. |
| ★ OLS ( Ordinary Least Squares Estimation) --> 통계적 회귀모델 |
선형회귀에서 결정계수를 계산하는 가장 보편적인 방법 | SSR(Sum of squared Residuals) 잔차제곱합이 최소가 되도록 선형회귀 모델의 파라미터 조정하는 방법 |
| 관계 | ||
| ★ Correlated | X값에 따라 Y값에 변화가 있을 때 Correlated 하다고 말한다. 얼마나 그 강도가 강한지도 계산할 수 있다. |
+ Positive correlation - Nagative correlation |
| ★ Causation vs Correlation | 원인과 연관성은 다르다. 연관성이 있다는 것이 영향이 나타나는 원인이 된다고 말할 수 없다. | |
Linear Regression
- 독립변수 1개 이상
- 독립변수가 종속변수에 얼마나 영향을 미치는지?
| 독립변수 | 주거공간(sqft_living) |
| 종속변수 | 가격 price |
1. 가정 Assumption
Q. 모형이 데이터를 잘 적합하는가?
모형이 데이터를 잘 적합하는지 확인하기 전에, 아래의 4가지 가정(Assumption)을 만족해야 한다.
가. 선형성 Linearity assumption
독립변수X의 변화에 따라 종속변수Y가 변화하는 모양이 선형이다.
- 확인 방법?
★ 산점도 그래프 : 시각화 해보는 것이 가장 정확하다.
★ 상관계수 : corr()
- python code
# 산점도 그래프
import seaborn as sns
sns.scatterplot(x=data['sqft_living'], y=data['price'])
data[['price', 'sqft_living']].corr()
>>> 강력한 양의 상관관계가 있다.
나. 정상성 Normality = 정규성
잔차항(residuals/errors)이 정규분포를 이룬다.
- 확인 방법?
★ quantile-quantile plot(QQplot) : 선에 가까울 수록 정규성을 띤다. 오른쪽 꼬리가 올라가면 왼쪽으로 치우친 데이터가 나온다.
★ Histogram of Residuals
★ Shapiro-Wilk 검정
<python code>
import matplotlib.pyplot as plt
# 밑바탕 준비하기
fig, axes = plt.subplots(1,2,figsize=(8,4))
# Histogram
sns.histplot(residual, ax=axes[0])
axes[0].set_xlabel("Residual Value")
axes[0].set_title("Histogram of Residuals")
# QQplot
sm.qqplot(residual, line='s', ax=axes[1])
axes[1].set_title("Normal QQplot")
# 그래프 공백 조절
plt.tight_layout()
plt.show()

# shapiro
# H1: 정규성을 만족한다/ H2: 정규성을 만족하지 않는다.
import scipy.stats as stats
from scipy.stats import shapiro
shapiro(residual)ShapiroResult(statistic=0.8369508981704712, pvalue=0.0)
>> 정규성을 만족하지 않는다.
다. 독립성 Independent Observations
잔차들 간에 상관관계가 없어야 하고, 잔차와 독립변수 값이 관련되어 있지 않아야 한다. 그러면 데이터 간에 서로 관련성 없이 독립이라는 것이 증명된다. 이것은 관찰된 값이 모두 독립적이며 상호 영향을 미치지 않음을 뜻한다.
- 확인 방법?
★ 데이터 수집과정 : 데이터가 어떻게 수집되어 있는지 파악하는 것이 중요하다.
★ Durbin-Watson 통계량 : 잔차항과 독립변수 값이 독립성을 만족하는지, 상관관계가 있는지 파악
| 0 | 2 | 4 |
| 양의 상관관계 | 독립성 만족 | 음의 상관관계 |
<python code>
# Durbin Watson
import statsmodels.api as sm
from statsmodels.stats.stattools import durbin_watson
durbin_watson(residual)1.9825552599878278model.summary()

>>>> 더빈왓슨 통계량이 2에 가까우므로 독립성을 만족한다.
라. 등분산성 Homoscedasticity
잔차항(residuals)과 예측값(Fitted Values) 간의 분포가 일정하거나 동일한 분산을 갖는다. 즉, random cloud 형태를 띄어야 한다. 만약 일정한 패턴을 보인다면 등분산성 가정에 위배되므로 다른 모델을 간구해야 한다.

- 확인 방법?
★ scatter plot : Fitted Values vs Residuals

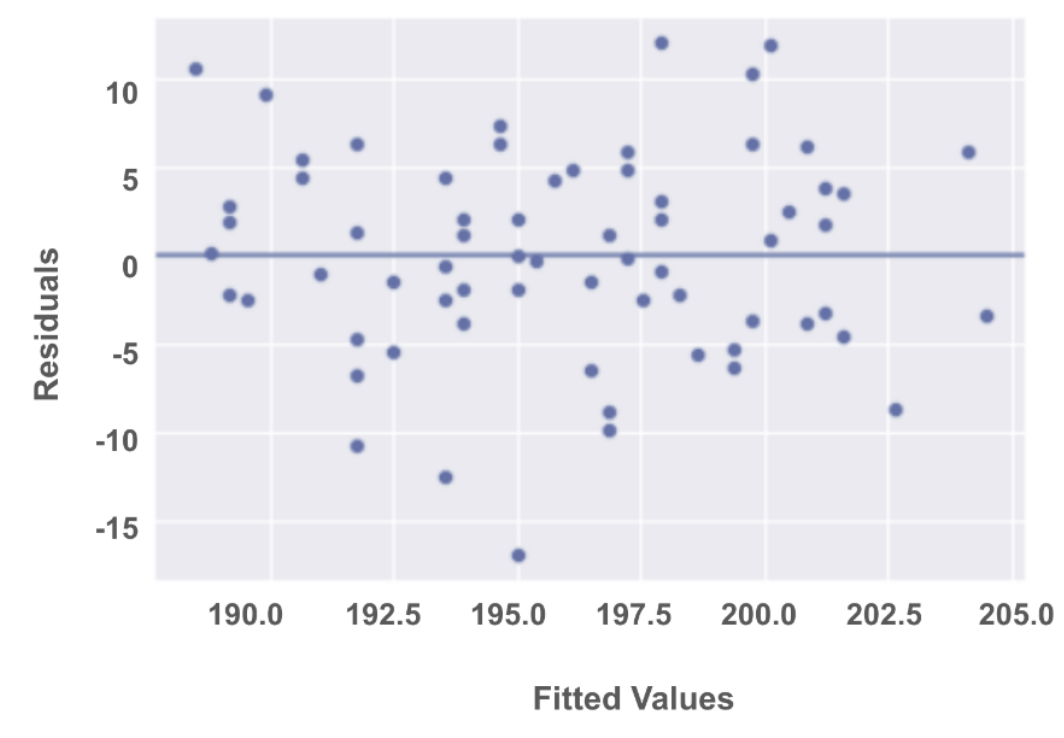
<python code>
# scatterplot, y=0
fig = sns.scatterplot(x= model.fittedvalues, y= residual)
fig.set_xlabel("Fitted Values")
fig.set_ylabel("Residuals")
fig.set_title("Fitted Value vs Residuals")
fig.axhline(0)
plt.show()
2. OLS 모델 만들기
continuous dependent variable(수치형 종속변수)와 1개 이상의 indendent variable(독립변수) 관계를 선형 관계로 나타낸다.
아래의 식으로 수많은 선을 그릴 수 있지만, 손실함수(loss function)를 가장 최소로 하는 best fit line을 그리고 싶다.
X: Predictor Variable
Y: Target Variable

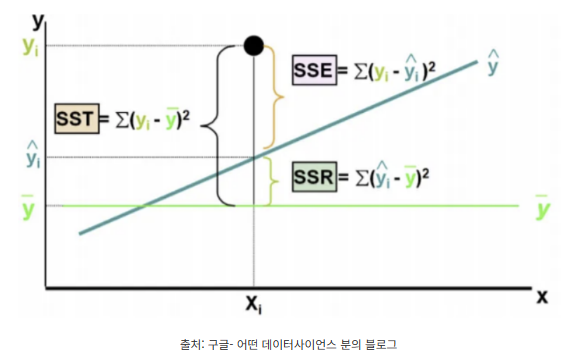
가. OLS ( Ordinary least squares estimation technique) 최소제곱추정량
SSR이 최소가 되도록 선형회귀 모델의 파라미터를 정하는 방법이다.

import statsmodels.api as sm
from statsmodels.formula.api import ols
formula = 'price~ sqft_living'
OLS = ols(formula= formula, data= data)
model = OLS.fit()
model.summary()
나. 회귀계수
model.paramsIntercept -43580.743094
sqft_living 280.623568
다. 예측값 FittedValue
# y_pred = Fitted value
y_pred= model.predict(data['sqft_living'])
y_pred= model.fittedvalues
y_pred0 287555.067025
1 677621.826402
2 172499.404187
3 506441.449985
라. Residual 잔차
이를 위해서는 에러를 찾아야 한다. 회귀선에서 예상하는 값과 실제 값의 차이를 뜻한다.
엡실론이라고 이름붙여보자.

# 잔차
residual= model.resid
residual0 -65655.067025
1 -139621.826402
2 7500.595813
3 97558.550015
4 82133.149027
...
마. SSR (Sum of squared Residuals) 잔차제곱합

mse = (residual**2).sum()/len(y_pred)
rmse = np.sqrt((mse))
rmse261440.79030067177
3. 통계적 유의 검정
Q. 회귀모형이 통계적으로 유의한가?
< 가설검정 >
H0: 회귀모형은 유의하지 않다. (B1=B2=...=BK=0)
H1: 회귀모형은 유의하다. (적어도 하나의 Bi는 0이 아니다)
< F통계량 확인 >
♡ F통계량이란?
회귀 모델의 적합도를 평가하기 위한 값
모델의 설명된 분산과 설명되지 않은 분산 간의 비율을 계산한다.
모델이 종속변수의 변동성을 얼마나 잘 설명하는지 측정한다.
(F통계량이 큰 값은 모델이 종속 변수의 변동성을 많이 설명하며, 작은 값은 설명력이 낮다는 것을 의미)
< Pvalue >
♡ Prob(F통계량)이란?
f통계량의 확률값이다. 즉, f통계량이 얼마나 통계적으로 유의미한지 나타내는 값이다.
유의수준(0.05) > pvalue : 귀무가설을 기각 --> 회귀모델은 유의하다.
유의수준(0.05) < pvalue : 귀무가설을 채택 --> 회귀모델은 유의하지 않다.

4. 회귀계수 유의성 검정
Q. 모형 내의 회귀계수가 유의한가?
회귀계수는 기울기를 의미한다. 기울기는 (y의 변화량/x의 변화량)이다. 따라서 값이 2개이므로 t통계량을 쓴다. 다시말해 회귀계수에 대한 t통계량의 pvalue로 통계적 유의성을 판단한다.
Confidence band 를 통해 모델의 부정확도에 관한 정보도 함께 제공한다.

5. 결정계수 R-square
Q. 모형은 데이터를 얼마나 설명하는가?

< 결정계수? >
회귀분석에서 종속변수 Y의 변동성이 독립변수 X에 의해 얼마나 설명되는지, 그 설명력을 나타내는 지표
결정계수 = 추정된 회귀식이 설명할 수 있는 데이터 / 전체 데이터

0 <R-squared <1 의 범위를 갖는다. 0이면 완벽히 다르며, 1에 가까울 수록 효율적인 모델이다.
| R² >=0.7 | 0.5<=R²<=0.7 | R²<0.5 |
| 모델의 설명력이 높다 | 모델이 중간 정도의 설명력을 갖는다 (종속변수의 일부 변동성을 설명하나, 미흡한 경우가 있음) |
음의 상관관계 (설명력이 낮거나, 모델이 적합하지 않을 수 있음) |

< 수정된 결정계수 >
Adjusted R-square : 다변량 회귀분석의 경우, 포함된 독립변수의 유의성과 관계없이 독립변수의 수가 많아지면 결정계수가 높아지는 경향을 보인다. 이를 보완한 것이 수정된 결정계수이다.
https://olivia-blackcherry.tistory.com/628
[ADP 데이터분석 전문가- 통계편] simple linear regression 선형회귀분석, 가정, 모델 분석과 평가
목차 1. 회귀분석 - 독립변수가 1개: 단순 선형 회귀분석 - 독립변수가 2개 이상: 다중 선형 회귀분석 * 문제 주거공간(sqft_living)을 독립변수, 가격(price)을 종속변수로 설정하여 단순 선형 회귀분석
olivia-blackcherry.tistory.com
https://olivia-blackcherry.tistory.com/593
[linear regression] residual, SSR, OLS, linear regression assumption, linearity, normality, independent observation, Homoscedast
목차 A technique that estimates the linear relationship between one independent variable X, and one continuous dependent variable Y. 1. Linear regression equation 방정식 1) Best fit line 아래 식으로 수많은 선을 그릴 수 있지만 우리는
olivia-blackcherry.tistory.com
https://olivia-blackcherry.tistory.com/483
model development, linear regression, plots, pipeline
1. simple linear regression will refer to one independent variable to make a prediction y= b+ax b: the intercept a: the slope fit X: Predictor variable Y: Target variable import linear_model from scikit-learn create a linear regression object using the con
olivia-blackcherry.tistory.com
