10차시 다중선형회귀분석(multilinear regression), 다중공선성, vif, 허용오차, variance_inflation_factor, ols, matrices, 변수선택법

 

Cars93 (1).csv

0.01MB

 
 

다중선형회귀분석 Multilinear regression

 
2개 이상의 독립변수가 종속변수에 미치는 영향을 추정하는 통계기법
실제 세상에는 독립변수가 2개 이상인 경우가 많다. 종속변수에 영향을 미치는 요인이 여러 개이기 때문이다. 이런 경우 독립변수가 종속변수에 미치는 영향을 수치화하고, 이를 토대로 미래를 예측하기 위해 다중선형회귀분석(Multi linear regression model)을 사용한다. 

 
 

Data preprocessing

 

# ' . ' 포함되어 있는 것은 OLS formula적용이 안됨. 
data.columns = data.columns.str.replace('.', '')
data.columns

Index(['Unnamed: 0', 'Manufacturer', 'Model', 'Type', 'MinPrice', 'Price',
       'MaxPrice', 'MPGcity', 'MPGhighway', 'AirBags', 'DriveTrain',
       'Cylinders', 'EngineSize', 'Horsepower', 'RPM', 'Revpermile',
       'Mantransavail', 'Fueltankcapacity', 'Passengers', 'Length',
       'Wheelbase', 'Width', 'Turncircle', 'Rearseatroom', 'Luggageroom',
       'Weight', 'Origin', 'Make'],
      dtype='object')

 
 

OLS

# OLS 모델 빌딩
import statsmodels.api as sm
import statsmodels.formula.api as smf
OLS= smf.ols(formula="Price~ EngineSize + RPM + Weight + Length + MPGcity +MPGhighway", data = data)
model= OLS.fit()
model.summary()

 

검토사항

1. 회귀모델 통계적 유의성

Q. 회귀모델이 통계적으로 유의한가?

< F 통계량 >

H0: 회귀모델이 유의하지 않다.
H1: 회귀모델이 유의하다.
 

<  AIC, BIC >

♡ AIC ?
Akaike information criterion 
모델의 상대적인 예측 성능을 평가하는 지표로 값이 작을 수록 좋다. 모델의 복잡도와 적합도를 함꼐 고려하여 모델 선택에 사용된다.
 
♡  BIC?
Bayesian information Criterion 
AIC와 유사하나, 모델 복잡도에 대한 패널티가 더 크게 적용됨. 단순한 모델을 선호함.
 
 
 

2. 결정계수 

Q. 모델은 데이터를 얼마나 설명하는가?

< Adjusted Rsquared > 

수정된 결정계수 확인하기
 
 

3.  회귀계수 통계적 유의성

Q. 모델 내의 회귀계수가 통계적으로 유의한가?

< T 통계량 >

H0: 회귀계수가 유의하지 않다.
H1: 회귀계수가 유의하다. 
모든 회귀계수가 유의한지 검정 후, 유의한 회귀계수로 식을 만들어 해석하기
 
 

4.  Assumption 

Q. 데이터가 전제하는 가정을 만족하는가?

data2 = data[['Price','EngineSize','RPM','MPGhighway']]
data2.head()

 

가. 독립변수와 종속변수 간 선형성

# Assumption 
#1. linearity
import matplotlib.pyplot as plt
import seaborn as sns

fig, axes = plt.subplots(1,4, figsize=(12,4))
sns.scatterplot(x=data2['EngineSize'], y= data2['Price'], ax= axes[0])
sns.scatterplot(x=data2['RPM'], y= data2['Price'], ax= axes[1])
sns.scatterplot(x=data2['MPGhighway'], y= data2['Price'], ax= axes[2])
sns.scatterplot(x=data['Length'], y= data2['Price'], ax= axes[3])

plt.tight_layout()

 

나. 오차의 정규성

# 2. Normality
residual = model4.resid
residual

0     -4.651687
1      7.396491
2      5.588074
3     14.188074
4      2.765553

 

import matplotlib.pyplot as plt
import seaborn as sns
fig, axes= plt.subplots(1,2, figsize=(8,4))

# Histogram
sns.histplot(residual, ax=axes[0])
axes[0].set_xlabel("Residual Value")
axes[0].set_title("Histogram of Residual")

# QQplot
sm.qqplot(residual, line='s', ax=axes[1])
axes[1].set_title("Normal QQplot")

 
 

다. 오차의 등분산성

# 3. Constant Variance 등분산성
fig= sns.scatterplot(x=model4.fittedvalues, y= model4.resid)
fig.axhline(0)
fig.set_xlabel("Fitted Values")
fig.set_ylabel("Residuals")
fig.set_title("Fitted Values vs Residuals")
plt.show()

 
 

라. 오차의 독립성

 
 

마. 다중공선성 No multicolinearity Assumption 

♡ 다중공선성이란?
모델의 일부 독립변수가 다른 독립변수와 상관관계가 높을 때 발생한다. 
(= 두 변수가 linearity하게 관련되어 있을 때 발생)
회귀계수의 분산을 증가--> 정확한 회귀계수 추정이 어려워짐
따라서 다중회귀분석 모델이 안정적이려면 두 개 이상의 독립변수들이 서로 밀접하게 관련되지 않아야 한다. 즉, 변수들이 linearity하게 관련되지 않아야 한다.
 
< 검사방법 >
1) 독립변수의 상관계수
corr()
0.9이상이면 다중공선성 높음

# 상관계수 -> 다중공선성 확인 
data.select_dtypes(include=[np.number])
data[['EngineSize', 'RPM', 'Weight', 'Length', 'MPGcity', 'MPGhighway']].corr()
# 상관관계가 0.9 이상이면 매우 높음
# EngineSize, Weight 0.84
# EngineSize, Lenght 0.78
# EngineSize, MPGcity -0.7
# Weight, Lenght 0.84
# Weight, MPGhighway 0.81
# MPGcity, MPGhighway 0.94

 
 
2) 허용오차
1-R²
한 독립변수의 분산 중 다른 독립변수에 의해 설명되지 않은 부분
0.1이하이면 다중공선성 높음
 
 
3) VIF 분산팽창요인(Variance Inflation Factors)
허용오차의 역수 

1~5	5<= VIF <=10	10 < VIF
다중공선성 낮음	주의 필요	다중공선성 높음

 
 
 
< 해결방법 >
- 다중공선성이 높은 변수 삭제
- 남은 데이터로 새로운 변수 생성
- 자료부족이 원인이라면 자료 보완
- Ridge 규제화를 통해 해결

# 5. 다중공선성
X= data2.drop(['Price'], axis=1)
y= data2['Price']
vif= [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
df_vif = pd.DataFrame(vif, index=X.columns, columns=['VIF'])
df_vif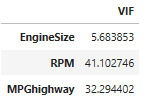

 
 
4) pvalue와 결정계수
결정계수 값은 높으나, 독립변수의 유의확률 값이 커서 개별 독립변수가 유의하지 않다면 다중공선성을 의심해봐야 함
 
< python code >
♡ dmatrices : 회귀식의 독립변수, 종속변수 출력

# 다중공선성 검사
from patsy import dmatrices
from statsmodels.stats.outliers_influence import variance_inflation_factor

#회귀식의 독립변수, 종속변수 출력
Y, X = dmatrices("Price~ EngineSize + RPM + Weight + Length + MPGcity +MPGhighway", data= data, return_type="dataframe")

 

 

X.columns[:3], X.values[:3]

(Index(['Intercept', 'EngineSize', 'RPM'], dtype='object'),
 array([[1.000e+00, 1.800e+00, 6.300e+03, 2.705e+03, 1.770e+02, 2.500e+01,
         3.100e+01],
        [1.000e+00, 3.200e+00, 5.500e+03, 3.560e+03, 1.950e+02, 1.800e+01,
         2.500e+01],
        [1.000e+00, 2.800e+00, 5.500e+03, 3.375e+03, 1.800e+02, 2.000e+01,
         2.600e+01]]))

 
 
♡  variance_inflation_factor( 위치, 컬럼번호)
vif확인한다. 10이상이면 다중공선성이 높다.

variance_inflation_factor(X.values, 4)

4.013002155745216​

 

 

전체 X컬럼에 대한 다중공선성을 확인한다.

vif_list = []
for i in range(1, len(X.columns)):
    vif_list.append([variance_inflation_factor(X.values, i), X.columns[i]])
vif_list

[[4.605118463185232, 'EngineSize'],
 [1.4468594016897707, 'RPM'],
 [8.685972560484025, 'Weight'],
 [4.013002155745216, 'Length'],
 [13.668287636879299, 'MPGcity'],
 [12.943132666343779, 'MPGhighway']]

 

 데이터프레임으로 나타낸다.

pd.DataFrame(vif_list, columns=['vif', 'column'])

 

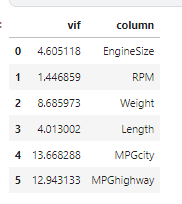
>>--> vif 값이 10 이상인 MPGcity와 MPGhighway 컬럼의 다중공선성이 높다. 그 중에서도 MPGcity가 가장 높다. 
 

# 변수제거
OLS2= smf.ols(formula="Price~ EngineSize + RPM + Weight + Length + MPGhighway", data = data)
model2= OLS2.fit()
model2.summary()

--> 결정계수는 0.569로 약간 높아졌고, 회귀계수 통계적 유의성이 높아졌다. 하지만 여전히 Length 0.823, Weight 0.121, MPGhighway 0.282로 유의수준보다 pvalue값이 높은 상황이다. 
 

# 유의확률이 높은 Length 변수제거
OLS3= smf.ols(formula="Price~ EngineSize + RPM + Weight + MPGhighway", data = data)
model3= OLS3.fit()
model3.summary()

 

# Weight 변수제거
OLS4= smf.ols(formula="Price~ EngineSize + RPM + MPGhighway", data = data)
model4= OLS4.fit()
model4.summary()

 
 

변수선택법

변수를 선택할 때는 F통계량, AIC 같은 특정 기준을 근거로 변수를 선택 또는 제거한다. 
F통계량이 높을수록, AIC가 낮을수록 좋다.
전진선택법/후진제거법/단계선택법이 있다.
참고로 요즘은 릿지, 라소, 엘라스틱넷을 이용한 규제화 방법을 사용하여 변수선택법을 현업에서 쓰는 추세는 아니다.

import time
import itertools
def processSubset(X,y, feature_set):
    model= sm.OLS(y, X[list(feature_set)])
    regr=model.fit()
    AIC=regr.aic
    return {"model": regr, "AIC":AIC}
    
    
# 전진선택법
def forward(X, y, predictors):
    remaining_predictors= [p for p in X.columns.difference(['Intercept']) if p not in predictors]
    results=[]
    for p in remaining_predictors:
        results.append(processSubset(X=X, y=y, feature_set=predictors +[p]+['Intercept']))
    
    models= pd.DataFrame(results)
    best_model= models.loc[models['AIC'].argmin()]
    print("Processed", models.shape[0], "models on", len(predictors)+1, "predictors in")
    print('Selected predictors:', best_model['model'].model.exog_names, 'AIC:', best_model[0])
    return best_model
    
    
# 후진소거법
def backward(X,y,predictors):
    tic= time.time()
    results=[]
    
    for combo in itertools.combinations(predictors, len(predictors)-1):
        results.append(processSubset(X=X, y=y, feature_set=list(combo)+['Intercept']))
    models= pd.DataFrame(results)
    
    best_model= models.loc[models['AIC'].argmin()]
    toc= time.time()
    
    print("Processed ", models.shape[0], "models on", len(predictors)-1, "predictors in", (toc - tic))
    print('Selected predictors:', best_model['model'].model.exog_names, 'AIC:', best_model[0])
    
    return best_model
    
    
 # 단계적 선택법
def stepwise_model(X, y):
    Stepmodels = pd.DataFrame(columns=['AIC', 'model'])
    tic= time.time()
    predictors=[]
    Smodel_before = processSubset(X, y, predictors+['Intercept'])['AIC']
    
    for i in range(1, len(X.columns.difference(['Intercept']))+1):
        Forward_result = forward(X=X, y=y, predictors=predictors)
        print('forward')
        Stepmodels.loc[i]=Forward_result
        predictors= Stepmodels.loc[i]['model'].model.exog_names
        predictors = [k for k in predictors if k !='Intercept']
        Backward_result= backward(X=X, y=y, predictors=predictors)
        
        if Backward_result['AIC']< Forward_result['AIC']:
            Stepmodels.loc[i] = Backward_result
            predictors= Stepmodels.loc[i]["model"].model.exog_names
            Smodel_before= Stepmodels.loc[i]['AIC']
            predictors= [k for k in predictors if k!= 'Intercept']
            print('backward')
            
        if Stepmodels.loc[i]['AIC']> Smodel_before:
            break
        else:
            Smodel_before= Stepmodels.loc[i]["AIC"]
    toc= time.time()
    print("Total elapsed time:", (toc-tic), "seconds")
    
    return (Stepmodels['model'][len(Stepmodels['model'])])

 
 
단계적선택법을 취하여 최적의 모델을 구하기

Stepwise_best_model= stepwise_model(X=X, y=Y)
Stepwise_best_model.aic

616.0976497740975

 

Stepwise_best_model.summary()

 
 
 
 
 
 

 

< 참고 url >

 
https://olivia-blackcherry.tistory.com/595

[multiple linear regression]No multicollinearity assumption, 다중공선성, VIF, interaction term, Ridge, Lasso, Elastic, feat

 
 
https://olivia-blackcherry.tistory.com/510

simple linear regression, multiple linear regression

 
https://olivia-blackcherry.tistory.com/629

[ADP 데이터분석 전문가- 통계편] 다중선형회귀분석, multi linear regression, 다중공선성, vif, 허용오차

 
https://olivia-blackcherry.tistory.com/596

[multiple linear regression] Python으로 다중회귀분석하기