목차
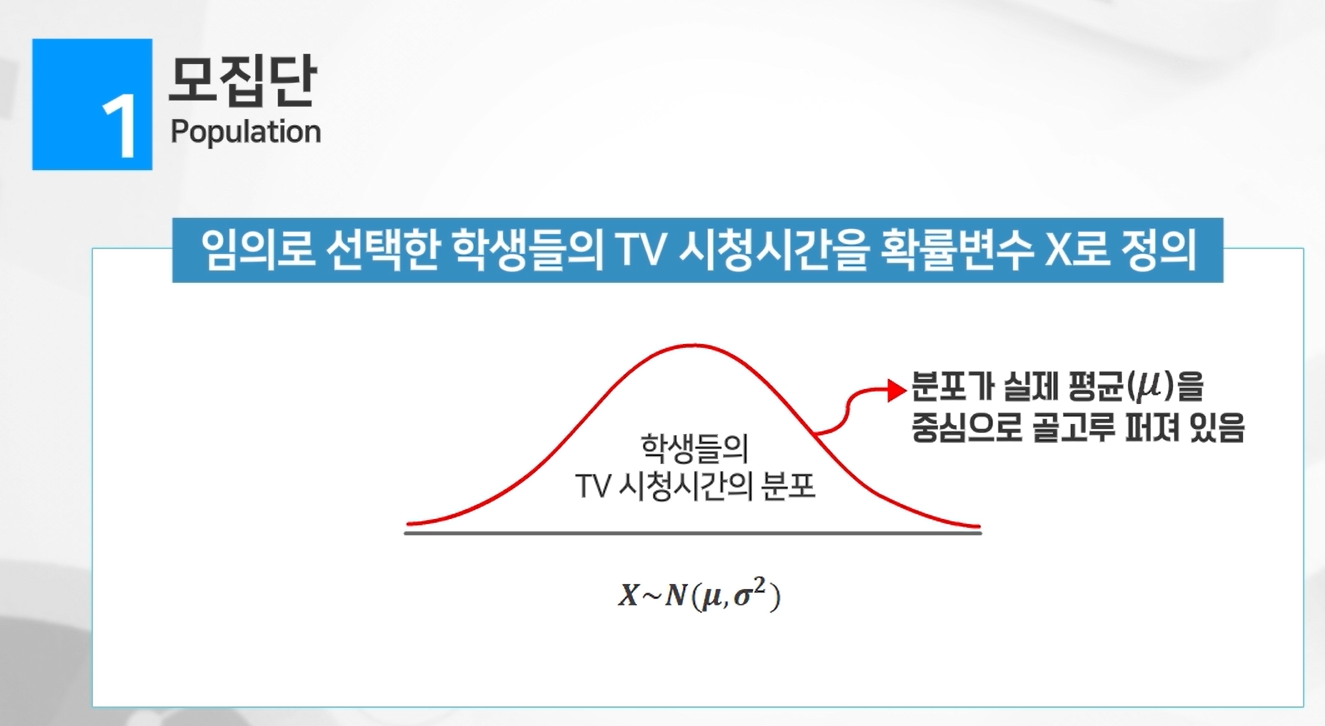
모집단
관심있는 연구 대상의 전체 집단
연구 대상의 특성에 대한 모든 값의 집합
모수 parameter
모집단의 특성을 나타내는 수

랜덤표본 random sample
집단의 일부를 표본이라 부르며,
모집단에서 독립적으로 뽑힌 표본을 랜덤표본 혹은 확률표본 또는 임의표본이라 함

iid : independent identically distributed 독립적으로 동일한 분포에서 표본 추출
X1~Xn은 서로 독립이고 동일한 분포를 따름
통계량 staticstic
표본으로부터 계산 가능한 표본의 특성값
랜덤표본의 함수로 통계량은 확률변수들의 함수이므로 확률변수임

표본분포
통계량의 확률분포를 표본분포라 함
ex) 표본평균의 분포, 표본분산의 분포, 표본비율의 분포
sampling distribution
통계량의 분포(표본의 분포X)로, 통계량이란 표본으로부터 계산되어지는 값이다.
표본평균들이 흩어지는 정도
표본평균의 분포
예컨데, 전교생이 1000명인 학교의 학생 중 50명의 학생들을 추출하여, 평균 하루 공부시간을 조사하였더니 10시간이 나왔다.
모집단: 전교생 1000명
모수: 하루 평균 공부시간
표본: 50명
통계량: 50명으로부터 계산되어진 값으로 50명의 하루 평균 공부시간
앞의 연구가 타당할까?
만약 50명의 다른 표본을 추출하면 하루 평균 공부시간이 10시간이 아니라 13시간이 나올 수도 있다.
이 연구가 타당하다고 말하려면, 표본평균들이 흩어진 정도가 얼마나 되는지를 밝혀줘야 한다.
그것이 곧 표본분포이다.

+표본평균의 분포
뽑힌 표본에 따라 값이 달라지므로 분포를 가진다.
+ 표본분산
뽑힌 표본에 따라 값이 달라지므로 분포를 가진다.
+통계량
표본평균, 표본분산과 같이 표본으로부터 계산 가능한 함수,
즉 표본에 따라 값이 변하는 확률변수
+표본분포
통계량의 분포
1) 모집단 X의 분포가 정규분포일 때, 표본평균의 분포도 정규분포를 따른다.


2) 임의의 모집단에서 표본평균의 분포
-> 정규분포를 따르거나, 따르지 않는 경우 모두
위와 동일하게 표본평균의 분포를 구할 수 있다.
-중심극한의 정리에 따라
중심극한정리 central limit theorem
임의의 모집단에서 랜덤표본의 평균의 분포는 표본의 크기가 충분히 클 때, 정규분포를 따른다.

'Certificate > 통계학' 카테고리의 다른 글
| [통계] 가설검정, 귀무가설, 대립가설, 제1종오류, 제2종오류, 유의수준, 가설검정의 절차 (0) | 2023.05.11 |
|---|---|
| [통계]통계적 추론, 추정, 가설검정, 점추정, 구간추정, 신뢰도, 신뢰구간, (1) | 2023.05.10 |
| [통계] 베르누이 시행, 이항분포, 정규분포, 표준정규분포, 표준정규분포표 (1) | 2023.05.10 |
| [통계] 확률변수, 확률분포, 이산확률변수, 연속확률변수, 모집단의 평균 분산 표준편차, 표본의 평균 분산 표준편차, 확률변수의 평균 분산 표준편차 (0) | 2023.05.09 |
| [통계] 확률론, 확률실험, 표본공간, 사상, 여사상, 배반사상, 독립사상, 순열, 조합, 조건부 확률, 전확률, 베이즈정리 (0) | 2023.05.09 |