ANOVA(Analysis of Variance)는 그룹 간의 평균 차이를 비교하기 위해 사용되는 통계적인 방법입니다. 주로 세 개 이상의 그룹을 비교하는 경우 사용되며, 그룹 내의 변동과 그룹 간의 변동을 분석하여 통계적으로 유의미한 차이가 있는지를 검정합니다.
ANOVA는 다음과 같은 가설을 설정하고 검정합니다:
귀무 가설(H0): 그룹 간의 평균 차이가 없다.
대립 가설(H1): 적어도 한 그룹의 평균이 다른 그룹들과 다르다.
★ ANOVA의 기본적인 아이디어
그룹 내의 분산과 그룹 간의 분산을 비교하여 그룹 간의 평균 차이가 랜덤한 것인지 아니면 insight가 있는 발생인지를 검정하는 것입니다. 만약 그룹 간의 변동이 크고, 그룹 내의 변동이 작을 경우에는 그룹 간의 평균 차이가 통계적으로 유의미하다고 할 수 있습니다.
★ ANOVA 종류
One-way ANOVA와 Two-way ANOVA
1) One-way ANOVA
One-way ANOVA는 한 개의 독립 변수(그룹 또는 처리 조건)를 기준으로 그룹 간의 평균 차이를 비교하는 방법입니다. 한 가지 요인에 따라 그룹을 구분하여 평균적인 차이가 있는지를 분석합니다.
예시: 세 가지 다른 교육 방법(A, B, C)을 시험 성적 향상에 적용하고자 합니다. 다음은 각 교육 방법의 성적 데이터입니다.
교육 방법 A: [85, 87, 82, 90, 89] (5명의 학생)
교육 방법 B: [78, 80, 83, 77, 85] (5명의 학생)
교육 방법 C: [92, 88, 95, 87, 90] (5명의 학생)import scipy.stats as stats
# 각 교육 방법의 데이터
method_a = [85, 87, 82, 90, 89]
method_b = [78, 80, 83, 77, 85]
method_c = [92, 88, 95, 87, 90]
# ANOVA 수행
f_statistic, p_value = stats.f_oneway(method_a, method_b, method_c)
# 결과 출력
print("F-statistic:", f_statistic)
print("p-value:", p_value)F-statistic: 9.009
p-value: 0.0012
★ F-value는 분석 결과에서 얻어지는 값으로, 그룹 간의 평균 차이가 랜덤한 변동에 비해 유의미한지를 나타내는 지표이다.
그룹 간의 분산과 그룹 내의 분산의 비율로 계산된다. f값이 크면 그룹 간의 차이가 통계적으로 유의미하다는 것을 나타낸다. 작은 경우 그룹 간의 차이가 랜덤한 변동으로 설명된다.
★ p-value는 통계적으로 유의미한지를 확인한다. 주어진 유의수준(일반적으로는 0.05)에 비해 작으므로, 그룹 간의 차이가 우연에 의한 것이 아니라 통계적으로 유의미하다고 알 수 있다.
결론: 적어도 한 그룹의 평균이 다른 그룹들과 다르다고 할 수 있다.
2) Two-way ANOVA
Two-way ANOVA는 두 개의 독립 변수(또는 요인)가 종속 변수에 영향을 미치는지를 분석하는 방법입니다. 두 가지 이상의 조건에 따라 그룹을 구분하여 평균적인 차이가 있는지를 분석합니다.
예시: 학생들의 시험 성적을 예측하기 위해 교육 방법과 학습 시간 두 가지 요인에 따른 시험 성적을 비교하고자 합니다. 다음은 각 교육 방법과 학습 시간에 따른 시험 성적 데이터입니다.
교육 방법 A, 학습 시간 X: [80, 85, 82] (3명의 학생)
교육 방법 A, 학습 시간 Y: [85, 88, 90] (3명의 학생)
교육 방법 B, 학습 시간 X: [75, 78, 80] (3명의 학생)
교육 방법 B, 학습 시간 Y: [80, 82, 84] (3명의 학생)
Python
데이터

1. 라이브러리 호출
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.multicomp import pairwise_tukeyhsd
2. boxplot
sns.boxplot(x = "TV", y = "Sales", data = data)
boxplot으로 TV변수에 대한 분포를 보니 변수의 값에 따라 Sales 분포도가 달라지는 것을 보니 이 변수를 고려해야할 만한 것으로 보인다.
이것이 통계적으로 유의미한 차이가 있는가에 대해서는 one way ANOVA test에서 확인해보자.
3. 모델 만들기
ols_formula = 'Sales ~ C(TV)'
OLS = ols(formula = ols_formula, data = data)
model = OLS.fit()
model_results = model.summary()
model_results

---> 결정계수는 0.874로 매우 높다. 이 모델이 Sales의 변동을 87.4% 설명한다는 것이기 때문에 매우 효과적인 예측을 한다고 본다.
----> 회귀 계수는 기본적인 것은 high이다. 나머지 low, medium은 high일 때보다 sales의 값이 작다.
----> p값은 0.000이므로 모든 회귀계수에 대해 통계적으로 유의미하다.
4. assumption test
1) linearity
- 변수가 continuous한 것이 아니기 때문에, 선형성은 보지 않아도 된다.
2) Independent observation
- 각각의 변수들이 독립적이기 때문에 독립성 가정에 만족한다.
3) normality
# Calculate the residuals.
residuals = model.resid
# Create a 1x2 plot figure.
fig, axes = plt.subplots(1, 2, figsize = (8,4))
# Create a histogram with the residuals.
sns.histplot(residuals, ax=axes[0])
# Set the x label of the residual plot.
axes[0].set_xlabel("Residual Value")
# Set the title of the residual plot.
axes[0].set_title("Histogram of Residuals")
# Create a QQ plot of the residuals.
sm.qqplot(residuals, line='s',ax = axes[1])
# Set the title of the QQ plot.
axes[1].set_title("Normal QQ Plot")
# Use matplotlib's tight_layout() function to add space between plots for a cleaner appearance.
plt.tight_layout()
# Show the plot.
plt.show()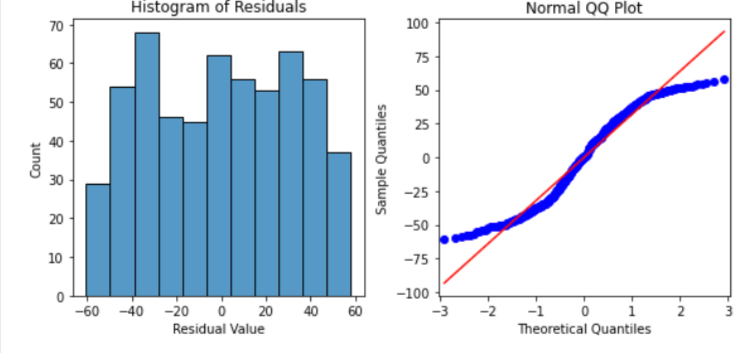
-> qqplot을 보면 파란색 선이 s자이기 때문에 정상성에 침해되는 것이라는 우려가 있기는 하지만, 우선 정상성이 만족된다고 가정하고 계속 진행한다.
4) Constant variance assumption
fig = sns.scatterplot(x = model.fittedvalues, y = model.resid)
# Set the x axis label
fig.set_xlabel("Fitted Values")
# Set the y axis label
fig.set_ylabel("Residuals")
# Set the title
fig.set_title("Fitted Values v. Residuals")
# Add a line at y = 0 to visualize the variance of residuals above and below 0.
fig.axhline(0)
# Show the plot
plt.show()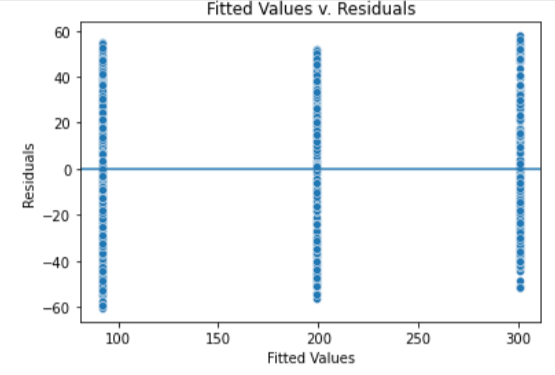
5. Perform a one-way ANOVA test
sm.stats.anova_lm(model, typ=1)
H0: TV홍보예산에 따른 Sales 결과는 다르지 않을 것이다.
H1: TV홍보예산에 따라 Sales 결과가 다르다.
F value 1971 ---> 집단 간 차이가 있다.
P value 매우작음 ---> 통계적으로 유의하다.
ANOVA test 결과로 H0은 기각하고, H1을 채택한다. 다시 말해, TV groups에 따라 Sales의 차이가 있으며 이는 통계적으로 유의하다.
6. Perform an ANOVA post hoc test
one way ANOVA 테스트에서 유의미한 결과를 얻었다면, 이번에는 post hoc test를 적용해보자. 예컨데 투키 HSD test이다. Tukey's HSD post hoc test는 TV 카테고리의 각각의 쌍에 대해 유의미한 차이가 있는지를 비교해주는 검정이다.
tukey_oneway = pairwise_tukeyhsd(endog = data["Sales"], groups = data["TV"])
tukey_oneway.summary()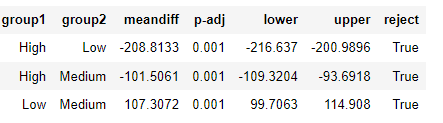
-----> 평균에서 차이가 있고, p value 역시 유의미하다. 따라서 귀무가설을 reject하는 것은 True이다.