목차
통계
문제를 정의하고 데이터를 수집한다. 데이터탐색 후 전처리, 변환 정제 과정을 거친 후, 통계모형을 수립한다. 수립한 통계모형이 적합한지 검정하고, 모형을 평가한 후 결론을 도출한다.
이번 시간에는 통계모형을 어떻게 수립하는지에 대해 ttest를 기본으로 공부해본다.
<절차>
검정 가설 설정(H0, H1)
유의수준 선택 (보통 5%)
p value 찾기( pvalue< 유의수준---> 귀무가설 기각)
ttest
독립변수 : 범주형
종속변수 : 연속형
ttest는 검정통계량이 귀무가설 하에서 t분포를 따르는 경우, 통계적 가설 검정 방법이다. 모집단 전체를 대상으로 검정을 진행하는 것이 아니라, 모집단 중 일부 표본을 따르는 경우 가설 검정 방법인 것이다. 표본의 크기(n)이 어느 정도 크다는 가정 아래(n>=30) 표본으로부터 산출되는 불편분산 s² 을 으로 모분산으로 σ² 간주하여 모평균 μ 를 추정한다. 만약 모집단분포가 정규분포라면, 이러한 가정 없이도 가능하다.

해석

가정
1) 정규성 Normality 만족하는가? --> Shapiro Test
2) 등분산성 Homogeneity 만족하는가? ---> Levene Test
단계
1) Test 그룹 나누기
2) Shapiro test, Levene test 하기
| normality | O | O | X |
| homogeneity | O | X | |
| t test(equal_var=True) | Welch test t test(equal_var=False) |
Mann Whitney U test |
★ Parametric Test 모수적 방법
데이터가 정규분포를 따른다는 가정 하에 수행되는 통계적 검정 방법이다. 정규성 가정을 만족하지 않는 경우 비모수 검정(non-parammetric test)를 쓴다.
종류

1. one sample ttest 일표본 t검정
단일 모집단, 특정 기준값과 비교
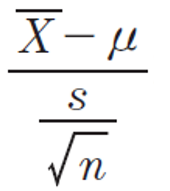
예) 어느날 우리반 몸무게의 평균이 2.3이 맞을까라는 의문이 들었다. 우리반 몸무게 평균은 2.3일까? 아닐까?
★ 통계적 물음 1차원 : 우리반 몸무게의 평균이 우연히 2.3일 확률은 얼마나 될까?
☆ 통계적 물음 2차원 : 우리반 몸무게 평균 2.3이 우연히 발생할 확률은 얼마나 될까?
<가정>
--> 정규성 만족하는가?
--> 등분산성 만족하는가?
<가설설정>
H0: 우리반 몸무게의 평균값은 2.3이다
H1: 우리반 몸무게의 평균값은 2.3이 아니다.
H0: 부산 aqi 평균은 10이하이다.
H1: 부산 aqi 평균은 10보다 클 것이다.
2. paired sample ttest 대응표본 t검정
단일모집단에 대해 어떤 처리를 함, 처리 전후에 따른 평균 차이 비교
표본 내 개체에 대해 두 번 측정하는 것
예) 어느 날, 1반 학생들의 몸무게(70kg)보다 2반 학생들의 몸무게(71.4kg)가 무겁다는 생각이 들었다. 두 반 몸무게는 같을까? 다를까?
★ 통계적 물음 1차원 : 두 반의 몸무게가 우연히 같을 확률은 얼마나 될까?
☆ 통계적 물음 2차원 : 두 반의 몸무게 차이인 1.4kg이 우연히 발생할 확률은 어떻게 될까?
★ 통계적 물음 3차원 : 두 반 몸무게 차이가 얼마나 커야 우연히 발생하지 않았다고 판단할까?
☆ 통계적 물음 4차원 : 1.4kg의 차이는 과연 큰 것일까? 작은 것일까?
---> 두 반 몸무게의 차이가 큰지 혹은 작은지 결정할 나름의 비교 대상이 필요하다. 우리는 그 비교 대상을 표준편차(분산)으로 한다.
★ 통계적 해석 1차원: 두 반의 데이터 사이의 평균 거리는 1.4kg이다. 그리고 두 집단 간 표준편차는 xxx이다. 따라서 만약 1.4kg이 표준편차보다 현저히 낮다면, 1.4kg에 큰 의미를 둘 수 없다. 하지만 만약에 표준편차보다 현저히 크다면, 두 데이터의 차이인 1.4kg 큰 의미를 둘 수 있다.
☆ 통계적 해석 2차원: t값과 t분포를 구한다.
<가정>
등분산성 만족함
--> 정규성 만족하는가?
<가설설정>
H0: 10명 환자 대상 영양제 복용 전, 후 수면시간 차이는 없다.
H1: 10명 환자 대상 영양제 복용 전, 후 수면시간 차이가 있다.
H0: 시험공부 전, 후 성적 차이는 없다.
H1: 시험공부 전, 후 성적 차이는 있다.
3. independent sample ttest 독립표본 t검정

Two sample ttest, AB test 라고도 불림
모집단, 모수, 표본이 모두 두 개씩 각각 존재
동일한 집단이 아니기 때문에, 등분산성 같은지 다른지가 매우 중요!
<가정>
---> 정규성 만족하는가?
-----> 등분산성 만족하는가?
H0: 1반 남학생 평균키, 2반 남학생 평균키는 같다.
H1: 1반 남학생 평균키, 2반 남학생 평균키는 다르다.
< 코드 >
모바일게임데이터이다. 게임 version이 gate 30/gate40인 사람들의 게임 횟수 및 유지율에 관한 데이터이다.
게임에서 첫 번째 게이트를 레벨 30에서 레벨 40으로 이동하는 A.B 테스트의 결과를 분석했고, 플레이어 유지율과 게임 라운드에 미치는 영향을 살펴봤다.


1. Package
# Base
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import os
# Hypothesis Testing
from scipy.stats import shapiro
import scipy.stats as stats
# Configuration
import warnings
warnings.filterwarnings("ignore")
warnings.simplefilter(action='ignore', category=FutureWarning)
pd.set_option('display.max_columns', None)
pd.options.display.float_format = '{:.4f}'.format
2. 그룹 나누기
where 함수 : 조건을 만족하는 배열의 인덱스 반환.
# Define A/B groups
ab["version"] = np.where(ab.version == "gate_30", "A", "B")
ab.head()
3. 가설설정
# A/B Testing Hypothesis
H0: A == B
H1: A != B
3. ttest python code
# A/B Testing Function 솔루션
# dataframe= 데이터, group = 검정하고자 하는 대상(특정컬럼이나 요소), target= 검정하고자하는 내용)
def AB_Test(dataframe, group, target):
# Packages
from scipy.stats import shapiro
import scipy.stats as stats
# Split A/B
groupA = dataframe[dataframe[group] == "A"][target]
groupB = dataframe[dataframe[group] == "B"][target]
# Assumption: Normality
# H0: Distribution is Normal! 정규성을 만족한다 - False
# H1: Distribution is not Normal! 정규성을 만족하지 않는다 - True
ntA = shapiro(groupA)[1] < 0.05
ntB = shapiro(groupB)[1] < 0.05
if (ntA == False) & (ntB == False): # "H0: Normal Distribution"
# Parametric Test
# Assumption: Homogeneity of variances
# H0: 등분산성을 만족한다.
# H1: 등분산성을 만족하지 않는다.
leveneTest = stats.levene(groupA, groupB)[1] < 0.05
# H0: Homogeneity: False
# H1: Heterogeneous: True
if leveneTest == False:
# Homogeneity
ttest = stats.ttest_ind(groupA, groupB, equal_var=True)[1]
# H0: M1 == M2 - False
# H1: M1 != M2 - True
else:
# Heterogeneous
ttest = stats.ttest_ind(groupA, groupB, equal_var=False)[1]
# H0: M1 == M2 - False
# H1: M1 != M2 - True
else:
# Non-Parametric Test
ttest = stats.mannwhitneyu(groupA, groupB)[1]
# H0: M1 == M2 - False
# H1: M1 != M2 - True
# Result
temp = pd.DataFrame({
"AB Hypothesis":[ttest < 0.05],
"p-value":[ttest]
})
temp["Test Type"] = np.where((ntA == False) & (ntB == False), "Parametric", "Non-Parametric")
temp["AB Hypothesis"] = np.where(temp["AB Hypothesis"] == False, "Fail to Reject H0", "Reject H0")
temp["Comment"] = np.where(temp["AB Hypothesis"] == "Fail to Reject H0", "A/B groups are similar!", "A/B groups are not similar!")
# Columns
if (ntA == False) & (ntB == False):
temp["Homogeneity"] = np.where(leveneTest == False, "Yes", "No")
temp = temp[["Test Type", "Homogeneity","AB Hypothesis", "p-value", "Comment"]]
else:
temp = temp[["Test Type","AB Hypothesis", "p-value", "Comment"]]
# Print Hypothesis
print("# A/B Testing Hypothesis")
print("H0: A == B")
print("H1: A != B", "\n")
return temp
# Apply A/B Testing
AB_Test(dataframe=ab, group = "version", target = "sum_gamerounds")
4. 결과

5. 결론
ab.groupby("version").retention_1.mean(), ab.groupby("version").retention_7.mean()(version
A 0.4482
B 0.4423
Name: retention_1, dtype: float64,
version
A 0.1902
B 0.1820
Name: retention_7, dtype: float64)레벨 30일 때 레벨 40일 때보다 1일 및 7일 평균 유지율이 높다.
< 추가적으로 더보기 >
[Hypothesis test] Python, scipy.ttest_ind(), scipy.ttest_1sample() (tistory.com)
[Hypothesis test] Python, scipy.ttest_ind(), scipy.ttest_1sample()
목차 문제 상황 서로 다른 구역에서 문맹률 차이가 나는데, 이것은 우연적인 것일까 아니면 통계적으로 유의미한 상황인 것일까? DistName에서 구역을 알 수 있고, Overall_li에서 문맹률을 알 수 있
olivia-blackcherry.tistory.com
[hypothesis test] 귀무가설, 대립가설, 유의수준, 유의확률, statistical significance, one-sampled test, two-sample
목차 ★ Hyptothesis testing 가설검정 A statistical procedure that uses sample data to evaluate an assumption about a population parameter. 샘플링된 데이터를 이용하여 모집단에 대해 설정한 가정을 평가하는 통계적 과정
olivia-blackcherry.tistory.com
[ADP 데이터분석 전문가- 통계편] t-test, 윌콕슨 부호순위, 샤피로, one sample ttest, paired sample ttest, ind
목차 통계파트 흐름 문제정의> 데이터수집> 데이터탐색 및 전처리> 데이터 변환/정제 >통계모형수립> 모형 적합검정> 모형 평가> 결론 도출 가장 중요한 것은 통계모형수립이다. 기초통계지식을
olivia-blackcherry.tistory.com